
| Command Post | August 24, 2007 |
If you have been following the PITCHf/x data this season, you've probably realized that the system has been implemented in more stadiums since the All-Star break, and is in 23 stadiums now. You've also probably noticed that the data provided from each stadium is slightly different. The velocity isn't very consistent between starts by the same pitcher in different stadiums, the movement of pitches seems to change and the release point has been shown to jump around as well.
The release point differences are the most important because as I learned last week, there are only nine parameters captured for each pitch. The three dimensional location of the ball, as well as acceleration and initial velocity, are all captured by the camera system, with the rest of the values that are shown, either in Gameday or the xml itself, being calculated from those nine values. Any discussion about how parks affect the speed or movement of pitches has to begin with a look at the data captured at release point. Below is a table that has the average release point height (in feet) for a team's staff, both at home and in all road stadiums. The way to read the table is that the average release height for all pitchers on the Red Sox while at Fenway was 5.30 feet, and was 6.08 feet for Red Sox pitchers on the road. One problem with using this method is that it doesn't use exactly the same group of pitchers for home and road, which is due to a lack of data, but it gives a rough idea of the release point height at each stadium.
Team Home Road Home-Road BOS 5.30 6.08 -0.78 SDN 5.61 5.83 -0.22 MIL 5.75 5.97 -0.21 CHA 5.61 5.81 -0.19 SLN 5.96 6.08 -0.12 CHN 6.20 6.31 -0.11 LAN 5.95 6.04 -0.09 SEA 5.81 5.89 -0.08 ARI 5.99 5.98 0.01 CLE 6.00 5.98 0.02 KCA 5.93 5.87 0.06 ATL 5.97 5.91 0.06 OAK 6.06 5.97 0.09 ANA 6.20 6.11 0.09 HOU 5.86 5.76 0.10 DET 6.03 5.91 0.12 TOR 5.79 5.65 0.14 TEX 6.43 6.29 0.14 CIN 6.32 6.17 0.16 PHI 6.33 6.11 0.23 MIN 6.18 5.95 0.23 COL 6.29 5.85 0.44 SFN 6.59 6.11 0.49
Most of the home heights are within .2 feet of their road data, with the exception of Boston, Colorado and San Francisco. However, even among these three stadiums, Fenway stands out, with the release point being .78 feet lower than the road. Every Red Sox pitcher had at least a .40 foot higher release point on road and looking at the average starting velocity of a pitch at each stadium, Red Sox pitchers throw 6.5 MPH faster on the road than at home. Clearly something is going on with the PITCHf/x system at Fenway and to a lesser extent at Coors and AT&T, and could be going on at other stadiums as well. Until we have confidence in the release points being tracked at every park, comparing data gathered at different stadiums without adjusting it will give misleading results.
Park Name Pit pfx_x(") pfx_z(") x0(') z0(') vy0(ft/s)
Home Josh Beckett 338 -4.19 3.47 -1.69 4.85 127.59
Road Josh Beckett 106 -4.51 8.36 -1.95 5.37 134.55
Home Manny Delcarmen 103 -5.93 7.28 -0.95 5.55 127.83
Road Manny Delcarmen 35 -4.07 10.07 -1.34 6.12 136.95
Home Eric Gagne 32 -2.14 3.01 -0.84 5.23 116.06
Road Eric Gagne 48 -3.54 9.03 -0.78 5.82 131.21
Home Jon Lester 97 0.96 4.27 2.98 5.66 117.52
Road Jon Lester 192 1.76 6.15 2.57 6.29 128.25
Home Daisuke Matsuzaka 314 -2.31 5.47 -2.08 5.14 123.67
Road Daisuke Matsuzaka 111 -3.56 9.06 -2.31 5.54 134.94
Home Hideki Okajima 71 2.60 8.02 -0.01 5.82 118.96
Road Hideki Okajima 27 3.34 6.38 -0.37 6.59 120.71
Home Jonathan Papelbon 64 -7.68 6.35 -2.28 4.98 132.33
Road Jonathan Papelbon 31 -6.57 9.84 -2.65 5.48 138.27
Home Kyle Snyder 87 -1.81 1.58 -1.51 6.22 112.67
Road Kyle Snyder 39 -1.69 6.28 -1.73 6.73 123.94
Home Julian Tavarez 248 -7.04 2.80 -1.70 5.16 122.88
Road Julian Tavarez 41 -6.90 5.31 -2.03 6.12 127.34
Home Mike Timlin 96 -3.50 6.91 -2.14 6.06 124.26
Road Mike Timlin 63 -2.86 8.44 -2.56 6.71 130.85
Home Tim Wakefield 316 0.88 1.98 -0.65 5.80 94.85
Road Tim Wakefield 71 3.03 3.65 -0.84 6.67 103.41
Looking at individual pitchers for the Red Sox, you can see how Fenway's camera system impacts the different pitchers. X0 and z0 are the coordinates for the release point, measured as a distance from the pitcher's body and from the ground respectively, and the release point is lower at home for all the pitchers. Almost all of the pitchers also get a smaller pfx_z value at home, which would seem to indicate that their pitches have more sink at Fenway, but is actually a result of the lower release height combined with the fact that, overall, the average height when a pitch crosses the plate at Fenway is similar to the height at other parks. The initial velocity is vy0, measured in feet/second, and is slower in every case. I didn't break this chart up by pitch, which is fine for examining the release points, but when looking at the velocity it gives an average that doesn't really mean anything.
Getting back to making an adjustment, the z coordinates of the release points are all roughly 10% too small at Fenway. If the Fenway x values were increased by 10% they would be a closer match for the release points on the road. However, once you make that adjustment, you need to adjust each of the other 8 parameters so that they are "measuring" at the new, adjusted release point, rather than the low release point. If you say that Fenway lowers the release point for every pitcher by 10%, and apply these adjustments to every pitch thrown at Fenway, here's what happens for Josh Beckett.
Park Name Pit x0 z0 vy0 Road Beckett 106 -1.95 5.37 134.55 Fenway Beckett 338 -1.69 4.85 127.59 Adj. Beckett 338 -1.99 5.39 136.53
Even through the adjusted numbers match the road numbers, I'm not very confident in using this method to make large-scale adjustments. For one thing, the road numbers could be off too. For Beckett I'm looking at one road start, made in Safeco, so I could be making too big of an adjustment. The lack of a large sample of road starts for pitchers is a major weakness of the type of separation I used in the home/road charts, but once there are more starts made in stadiums with the pitch f/x system, that hopefully can change. I think any true park factors are going to need to wait until there is more data captured at all stadiums.
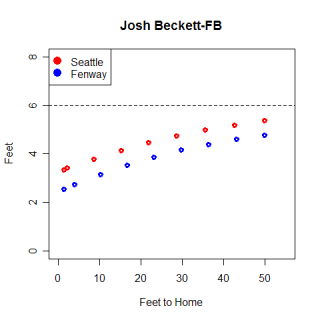
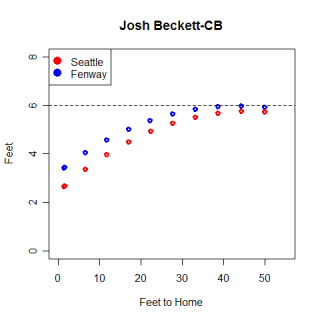
Here are two graphs of a randomly selected Beckett fastball and curveball at Fenway and Safeco, as viewed from the first base line. You can really see the difference that the release height makes from this view. There appear to be some differences in how the curveball moves at the different stadiums, but the fastball follows virtually the same path, just at different heights, in both cases. Each dot represents the ball's position in .05 second intervals, which segues nicely into my last section.
I received a comment yesterday on my article from last week that suggested a better way to quantify the speed of a pitch was to determine how far away the pitch is when the batter has to decide whether to swing. It probably is even more intuitive to think of it like this compared to how many seconds the ball takes to arrive, so I went ahead and calculated some distances.
You can test your reaction time here, and after some extensive research (emailing the link to five friends) I think a rough proxy for an MLB reaction time is around .2 seconds. If a pitch takes .513 seconds to reach the plate, as a Wakefield knuckleball does, then the hitter can let the pitch travel for .313 seconds out of Wakefield's hand before making a decision. The pitch is 19.75 feet from home plate at .313 seconds, so the hitter can wait until Wakefield's knuckleball is about 20 feet from him before making a decision. A hitter has to make a decision on a fastball on a Beckett fastball 27 feet from home, while on a Rich Hill curveball the hitter has to decide when the pitch is 21 feet from home.
The hard part of finding these numbers is determining the reaction time. The test above only involves clicking a mouse button, which is nearly instantaneous, but swinging a bat takes much longer. Even if the hitter had a reaction time of .2 seconds, once he recognized the pitch and reacted, actually swinging the bat would take some time as well. If you add on another .1 second to account for the swing, the distances are pushed back to 29 feet for Wakefield's knuckleball, 41 feet for Beckett's fastball, and 31 feet for Hill's curve.
I have no idea if the .1 second swing time is accurate, but at 41 feet from the plate most pitches look very similar. Hill's curveball hasn't began to break yet and it looks very similar to Beckett's fastball. If you had a reaction time of .2 seconds and a swing that lasts .2 seconds after the reaction time, you would need to artificially speed up your reaction time and decide whether to swing at Beckett's fastball before he even released his pitch. If he were throwing his curveball or changeup instead...well, Beckett does have 148 strikeouts this year. I believe there is some overlap on reaction time and when the swing begins, which lowers the overall time used, and I think there is also some element of "Blink" involved here, where good hitters "know" to swing at a pitch before they realize why they are swinging at it. Either way, hitting is hard.
Comments
Quick question
Im kinda in the processing of learning "R" and i was wondering how to import the xml gameday files into R
John
Posted by: john at August 26, 2007 9:23 AM
John, I am a fellow R beginner. I import my gameday data into R from a MySQL database, so I'm not exactly sure how to bring the XML straight in, but I'm guessing you'd need to install an XML parser plug-in for R, like the one here:
http://www.omegahat.org/RSXML/Overview.html
I couldn't find anything in the R documentation itself about XML.
Posted by: Mike Fast at August 27, 2007 9:00 PM
I installed some packages for XML in R but I still couldnt figure it out.
I suppose I could do it your way but im relatively new to MySQL as well lol.
Posted by: john at August 28, 2007 5:16 AM