
| Designated Hitter | November 08, 2007 |
Sometimes I think most baseball strategy has been figured out thanks to sabermetricians like you and me. Then I discover that a major facet of the game is being mismanaged at a shocking rate.
Let me explain. I recently undertook a study to analyze the importance of outfield arms, starting with centerfielders. I used Andruw Jones as a case study to determine how many baserunners he’s able to prevent from advancing compared to the average centerfielder. What I learned was that Jones, generally regarded as having one of the best outfield arms in baseball, only prevented 9 runners from advancing in 247 chances last year compared to the average centerfielder. Why so low? Is it because Jones doesn’t have such a feared arm after all? Certainly not. Instead it appears baserunners are incredibly reluctant to advance on anybody; basically only taking the risk when it’s a sure thing. Here’s how I came to that conclusion.
Using Retrosheet data from 2006, the success rate of runners attempting to advance on a ball hit to centerfield with less than two outs is seen in the following table.
Less Than 2 Outs Chances Attempted Out Success
Advance Trying Rate
----------------------------------------------------------------
1st to 3rd on single 1079 305 6 .98
2nd to home on single 1039 700 22 .97
1st to home on double 469 243 13 .95
1st to 2nd on flyball 1385 23 2 .91
2nd to 3rd on flyball 1008 360 11 .97
3rd to home on flyball 689 599 15 .97
Total 5669 2230 69 .97
Notice how 61% of baserunners don’t even try for the extra base with less than 2 outs. Of those who challenge the outfielder, only 3% get thrown out, and only 1% of all baserunners facing the decision of whether or not to advance get gunned down. That’s what I meant when I said they take the risk only when it’s a sure thing.
Here’s the same chart with 2 outs.
Less Than 2 Outs Chances Attempted Out Success
Advance Trying Rate
----------------------------------------------------------------
1st to 3rd on single 699 262 3 .99
2nd to home on single 813 784 33 .96
1st to home on double 304 225 8 .96
Total 1816 1271 44 .97
So with two outs and the runners moving on contact, and in a situation where one would expect to see additional risks taken because of the greater possibility of stranding runners, the success rate is the same at 97%.
There are three possible explanations for the high overall success rate. One is the possibility that runners and coaches are extremely reluctant to try and advance for fear of getting thrown out and the shame that comes with it. Certainly, being thrown out can be a rally killer, but a 1% failure rate is almost like taking no risk at all.
Another explanation is the extreme difficulty in throwing a runner out from centerfield. Consider all the unlikely things that must happen for a runner to be thrown out. First the defender must field the ball cleanly, then hit the cutoff man with a strong throw, or throw a strike from the outfield to the base in question. If cutoff, the infielder then needs to turn and throw a strike, usually from the outfield grass, without first looking. If all these things go right, there’s still a chance the ball might hit the baserunner. If not, the fielder needs to catch it cleanly, often on a hop, position himself properly and apply the tag. A play at the plate brings additional challenges. A ball thrown from centerfield frequently hits the pitcher’s mound knocking it offline or slowing it down, while the catcher must try and block the plate and brace himself for a collision while still making the catch and applying the tag.
The final possibility is that centerfielders as a whole don’t possess exceptionally strong throwing arms. Rightfielders tend to have the strongest arms because of the need to make the long throw to third base. Also, the prototypical centerfielder is slender and swift, hardly the type of ballplayer known for a cannon arm (yes, I’m referring to you Juan Pierre and Coco Crisp). Ichiro is the exception that makes the rule although he was a rightfielder for his entire MLB career until late in 2006.
Of the three possible explanations for a 97% success rate, the second and third go hand in hand connoting a degree of difficulty that is undeniable. But, given the difficulty of the task, wouldn’t baserunners be more inclined to take the risk? Which brings us back to explanation #1 – there must be a decided reluctance among runners and coaches to try for the extra base.
How reluctant are they and what is the right amount to run? For that we turn to a methodology frequently used to analyze the value of the stolen base. It’s based on the Run Expectancy table here, i.e. the number of runs one can expect for the remainder of an inning given the number of runners on base and the number of outs. From the table, one can calculate the break-even point for various strategies. For instance, if staying put on a base is expected to yield 1.2 runs for the remainder of an inning, and going for the extra base increases the yield to 1.4 runs, but the result of getting thrown out would decrease the expectancy to 1.0 runs, then the risk is equal to the reward and the break-even point is a 50% success rate.
Using that methodology, the generally accepted break-even point for stealing second base is between 67% and 75% as described in this Baseball Analysts article earlier in the season. This type of analysis is common for stolen bases and bunts, but to my knowledge has never been published for runners trying to advance on batted balls - until now.
The graph below shows all the possible scenarios and break-even points for 0 outs and 1 out compared to the actual success rate for each situation.
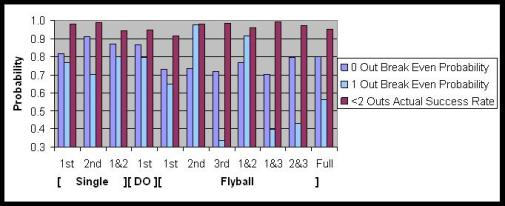
Notice how the break-even points are usually lower with one out than with no outs. This implies that runners should take more risks later in the inning, which makes sense because the more outs there are, the greater chance of a runner getting stranded on the bases. The exception appears to be when a runner is trying for 3rd on a flyball. In that situation, he should be more cautious with one out than with no outs.
Also, the break-even point can be wildly different depending on the number of outs. For instance, with a runner on 3rd and nobody out, the break-even point on a flyball to centerfield is .72 (the flyball being the first out), whereas with one out (two outs after the flyball is caught) the break-even point is a miniscule .34. The break-even analysis indicates that coaches should send guys from 3rd almost every time on a flyball to center with one out. Even if they’re thrown out 65% of the time, the net result will be positive. Basically the risk of sending a dead duck to the plate is worth it compared to relying on the next batter to knock the run in. And yet, the actual success rate in that situation is an incredible 98%! The chart visually depicts that in every situation the actual success rate far exceeds what one would expect using break-even analysis.
Clearly the run environment has a lot to do with break-even points. This includes the ballpark, the stinginess of the pitcher and defense, the score of the game, and the ability of the upcoming batters to drive runs in. Runners should be more cautious with big boppers hitting behind them, while they should be more aggressive toward the bottom of the batting order. Dan Levitt has a good discussion of run environments in his analysis of bunting here. For the sake of simplicity, this analysis ignores the run environment and looks at the situation as a whole, based on a season’s worth of data.
It’s somewhat ironic how the prototypical batting order has the speedy guys up front who would naturally be more aggressive baserunners, followed by the run producers who create a run environment where the speedy guys should be less risky on the bases. I guess I subscribe to the theory that those with the highest OBP should bat in the #1 and #2 spots regardless of how fast they are. But, that’s another topic for another day. Now back to the issue at hand.
With two outs, the chart is simpler because of the absence of runners advancing on flyballs, and looks like this:
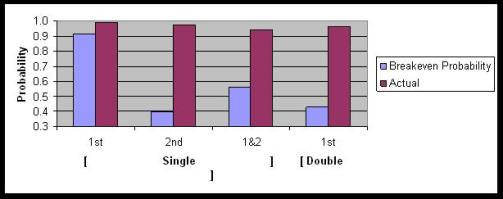
When trying to score with 2 outs, the break-even probability is between .40 and .55 depending on the situation, while the actual success rate is well north of .90! Once again, the chart indicates that the actual success rate is significantly higher than the break-even value for every situation. This data reinforces my previous verdict that runners/coaches are phenomenally risk averse when it comes to taking the extra base.
For as long as I can remember, baseball announcers were always warning fans that it’s a mortal sin for ballplayers to make the first or third out at 3rd base. The data above tests that claim and supports half of the general tenet. With two outs, the highest break-even mark is at 92% when a runner tries for 3rd on a single. Similarly, the first graph showed us that runners trying to advance to 3rd on a flyball caught for the second out have break-even rates of 97% with a runner on 2nd and 92% with runners on 1st and 2nd. So it’s clear that making the final out at 3rd with two outs is not recommended. However, with nobody out, the story is different. Runners trying to advance to 3rd have a break even rate of 81%, but runners trying to score have break-even rates of 91% or 87% depending on the situation. So it appears that the greater sin is getting thrown out at home with nobody out, not at 3rd.
Although my analysis was conducted using only balls hit to centerfield, the results appear to be similar for hits to left and rightfield. According to Dan Fox in his 3-part series on baserunning here, the total success rate from 2000-2004 is .94 for balls hit to leftfield and .96 for balls hit to right not counting runners advancing on flyball outs. It should also be noted that the break-even numbers are conservative estimates. The actual break-even value is lower than indicated because the analysis ignores the possibility of trailing runners advancing on a throw, or of a throwing error allowing a runner to take an extra base. Finally, the analysis doesn’t look at singles stretched into doubles, doubles into triples, or triples into inside-the-park homers because the Retrosheet information doesn’t lend itself to that level of detail. Assuming similar reluctance and success rates, one can extrapolate the information to conclude that the total impact of runner’s reluctance is significantly higher than any estimate based only on baserunners trying to advance.
In conclusion, this is what we know so far:
1. Runners and coaches are extremely reluctant to go for the extra base on centerfielders
2. This “runner’s reluctance” applies not only to balls hit to centerfield as studied here, but to left and rightfield as well
3. Break-even analysis indicates that actual success rates are universally higher than break-even rates
4. In general, runners should take more risks as the number of outs increase
5. Runners should be the most cautious when trying for 3rd with two outs, or when trying for home with zero outs (not 3rd as the old adage states)
6. With two outs, runners should try for home even if the failure rate is greater than 50%.
What we don’t know is the impact of runner’s reluctance relative to runs scored and wins. For that you’ll have come back tomorrow for Part Two of the analysis.
Ross Roley is a lifelong baseball fan, a baseball analysis hobbyist, and former Professor of Mathematics at the U.S. Air Force Academy.
Comments
Excellent article, but there may be one other potential explanation for the very high success rates of advancing (not that I necessarily believe it). Base coaches and base runners could be very good at identifying particular instances that would result in an out. Put another way, sending a runner in one of these risky situations may have a marginal success rate under the break even point. This marginal rate would be a more accurate measure than the total rate which includes opportunities to advance with very little risk.
Posted by: Craig at November 8, 2007 7:01 AM
Ross,
Excellent article!!! One thing your study can't possibly track is the reluctance to take the extra base on line drive hits that to CF that are close to being caught by the SS/2B or the CF. In other words, runners are more likely to play it station to station on these type of hits. That would hold down the number of attempts to take the extra base and result in better success ratios when they do attempt to take the extra base on the "sure thing" type of hit. Also, a guy like David Ortiz if not normally going to test the CF much unless it's hit in the "sure thing" zone, but Jose Reyes make take more chances on balls hit into a riskier zone. Maybe there is a way to look at what zone the ball landed and calculate that success rate?
Mike
Posted by: Mike Pinciaro at November 8, 2007 7:37 AM
The problem is you have alot of noise in your "opportunities" to advance. There are tons of cases where you have a superfast runner (Ichiro, Pierre, Crawford, whoever) that will simply not take the extra base, because he'd be thrown out by 10 feet. If these runners go from 1B to 3B on a single with 0 outs 50% of the time, it's extremely likely that at least 40-45% of all "opportunities" are not opportunities at all.
At the other end are the easy "opportunities". These are plays where even the slowest runners will make it. Perhaps 10-15% of all opps in the above case are freebies. What you are left with is about 35-40% of the "opportunities" are actually discretionary. And it's on that basis that you need to evaluate the runners.
Posted by: tangotiger at November 8, 2007 7:39 AM
You might find this link useful:
http://www.tangotiger.net/destmob1.html
Posted by: tangotiger at November 8, 2007 7:42 AM
Your article focuses on the break-even point, which I take to be the probability of success at which taking the base is neutral to not taking the base. But I take the result to mean that on *any individual play* if you have a better chance than the breakeven (putting aside situational complications etc.), you should take it. That means you should take your chances only when your probability equals the breakeven OR greater. Over the course of a large number plays, a team that employs this strategy perfectly, however, would have an overall average success rate that is GREATER than the breakeven, because many of the plays they ran on had greater than breakeven chance of success.
I think this is a problem with looking at aggregate rates in evaluating basestealers too. A guy who steals at the overall average rate of breakeven is probably taking too many "lower than breakeven chances" which are averaged out by the "no brainer or greater than breakeven" opportunities he does take.
Posted by: Tony Candido at November 8, 2007 7:54 AM
I should add, that regardless, 97% seems WAY too high.
Your result IIRC is consistent with analysis in many sports that coaches/players don't maximize the chances of winning when doing so involves a play with visible downside, i.e., basketball teams down by 2 point at the buzzer don't take enought 3-point shots; football teams don't go for it on 4th down enough etc.
Posted by: Tony Candido at November 8, 2007 8:02 AM
It is very interesting that so many fewer runners attempt to go first to third on a single to center with one out than those who attempt to score from first on a double to center with one out.
Remembering that some (most?) of the first-third attempts occur on the hit-and-run, there is a valid inference that runners are too cautious. I suspect that part of the issue is avoidance of responsibility. On the double, the third base coach makes the call whether to go and if the runner is thrown out, he is simply "following orders". On the single, the play is in front of the runner and if he is thrown out, he takes the heat in the dugout. For some reason, getting thrown out on a single generates more heat than a failed attempt to steal a base.
Posted by: Mike Green at November 8, 2007 8:20 AM
One explanation - close tag plays on the basepaths, especially collisions at home, probably have the highest probability of injury for any play in baseball. The added value of the advancement pales in comparison to the cost of a weeks-long DL stint. Adding injury cost to the cost of the out might make the break-even probability very close to 1.
Also, running into an out means fewer pitches thrown by the pitcher per out, and fewer at-bats for your best hitters in the long run. These additional costs have to be evaluated as well, though may be partially incorporated into the run expectancy matrix.
Posted by: Larry at November 8, 2007 9:28 AM
I think Tony makes the essential point here: our expectation is that the success rate will be far higher than break-even, if teams only attempt the extra base when chance of success >= break-even rate. So high success rates alone don't tell us much (though these rates are so high that it does seem likely that teams are too conservative).
One way to evaluate the decision-making is to compare break-even points to attempt%, rather than success rate. Do teams attempt the extra base when they should? And it looks like they generally do. For example, on FB,
Posted by: Guy at November 8, 2007 10:41 AM
Hmm, not sure what happened there. Continuing.....
One way to evaluate the decision-making is to compare break-even points to attempt%, rather than success rate. Do teams attempt the extra base when they should? And it looks like they generally do. For example, on FB, less than 2 out, runner on 2B, the break-even is very high (around .85) and just 36% of runners try for 3B. But with runner on 3B, break-even drops to about .55, and 87% of runners try for home.
The problem with using success rate as your barometer is most clear with runner on 2B, 2 outs, single. You can't fault teams for an 'excessive' success rate of 96%, when 96.4% of runners head for home. Surely most of the other 3.6% are infield hits or other situations where reaching home is very unlikely. And even if every one of these 3.6% ran and made out, the success rate would still be 92.4.
Posted by: Guy at November 8, 2007 10:59 AM
Others have been more eloquent, but in simple terms, the 97% success rate measures the ability for the ball-player to quickly analyze his chances of taking the extra base. It shows that ball players are very good at sizing up the situation on the fly. I'm not so sure how accurately one can apply this data to infer missed opportunities. One would think that this is a scenario of diminishing returns, showing an exponential relationship towards failure the more times you try for the extra base. I would also venture also that the data points to the knee of this curve – and that runners intuitively sense this.
Obviously if we had stats for a season where ball players HAD to take the extra base, you could compare the two sets of stats and graph the relationship. The closest fit that I can think of to this type of season was when newly hired manager John Russell was the 3rd base coach for the Pirates a few years back. He waived everyone home.
Posted by: C.P. from NJ at November 8, 2007 11:28 AM
I've done some similar work on the topic. I personally chalk it up to an imbalance in 3rd base coaches risk/reward schedule. If the coach sends the runner and he's safe, the runner gets credit for being fast. If the coach sends the runner and he's out, the coach gets blamed for being a moron. Too many "mistakes" and the coach gets fired, even if he's actually increasing his team's chances for scoring runs. I'm of the opinion that third base coaches should be replaced with a sign that says "Greetings, runner entering third base. If the gentleman holding the ball right now is currently an outfielder, please turn left and run an additional ninety feet. And batter, for the love of God, don't bunt unless you are just an awful awful hitter!"
Posted by: Pizza Cutter at November 9, 2007 8:13 AM