In Part One of this two-part series we explored the reluctance of runners and coaches to take risks on the basepaths, discovering that 97% of those attempting to advance on centerfielders were successful in 2006 while the break-even point is significantly lower than the actual success rate for every conceivable situation. I concluded in that article that runners and coaches were incredibly risk averse. In this article I will attempt to quantify the lost opportunity associated with this conservative strategy.

The numbers from 2006 tell us that less than half (47%) of baserunners attempted to advance on balls hit to centerfield while 97% were successful. From that existing state, let’s imagine that 3rd base coaches start sending runners more frequently in an attempt to take more chances and score more runs. One can easily surmise that the success rate would steadily go down as more runners take the chance. In Economics, this is referred to as the Law of Diminishing Returns. Let’s assume that for each additional 1% of attempts (which rounds to 75 runners), the success rate drops by 1%. So the first 75 guys succeed at a 96% rate, the next 75 at 95% and so forth. The chart below graphically frames the problem under discussion. It shows what this notional curve would look like (in green) compared to a break-even level of 71% (red). Also included in the graph is a purple line showing what would happen if every additional runner were thrown out and another line in blue showing what would happen if the rest of the attempts were at the break-even rate of 71%.

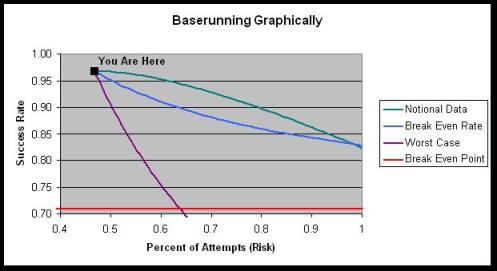
Notice how 17% more baserunners would have to take the risk and all of them get gunned out before the overall success rate equals the break-even point of 71% (where the purple and red lines intersect). Obviously it wouldn’t be advisable to send 17% more guys knowing they would all get thrown out. In fact, it wouldn’t be advisable to send any runners who had a 0% chance of success. Instead, a coach should theoretically send anyone whose chance of success is better than the break-even rate of 71%. So any curve above the blue line would result in a positive number of runs scored.

To estimate the number of additional runs that could be scored if runners and coaches were more aggressive, we examine the notional data more closely. Going back to the Expected Run table introduced last time, the weighted average of outcomes where a runner is successful in trying for the extra base comes out to .29 additional runs for the remainder of an inning (the reward), while failures cost .71 runs on average (the risk). Coincidentally, .71 and .29 add to 1.00 and the break-even rate happens to be the same as the risk, i.e. .71. Using these values for risk and reward, the table below calculates the net runs scored by each set of 75 attempted baserunners.

Notional Data – If Runners Were More Aggressive

Runners     Success    Number       Successes    Failures      Net Runs
            Rate       Thrown Out   (*.29)       (*-.71)
---------------------------------------------------------------------------
75          0.96        3           20.9         -2.1          18.8
75          0.95        4           20.6         -2.8          17.8
75          0.94        5           20.3         -3.6          16.7
75          0.93        5           20.3         -3.6          16.7
75          0.92        6           20.0         -4.3          15.7
75          0.91        7           19.7         -5.0          14.7
75          0.90        8           19.4         -5.7          13.7
75          0.89        8           19.4         -5.7          13.7
75          0.88        9           19.1         -6.4          12.7
75          0.87       10           18.9         -7.1          11.8
75          0.86       11           18.6         -7.8          10.8
75          0.85       11           18.6         -7.8          10.8
75          0.84       12           18.3         -8.5           9.8
75          0.83       13           18.0         -9.2           8.8
75          0.82       14           17.7         -9.9           7.8
75          0.81       14           17.7         -9.9           7.8
75          0.80       15           17.4        -10.7           6.7
75          0.79       16           17.1        -11.4           5.7
75          0.78       17           16.8        -12.1           4.7
75          0.77       17           16.8        -12.1           4.7
75          0.76       18           16.5        -12.8           3.7
75          0.75       19           16.2        -13.5           2.7
75          0.74       20           16.0        -14.2           1.8
75          0.73       20           16.0        -14.2           1.8
75          0.72       21           15.7        -14.9           0.8
Totals
1875        0.84       303         456.0       -215.3         240.7

Notice the Law of Diminishing Returns in action in the far right column, with fewer and fewer net runs scored as the success rate goes down. The table also reinforces my earlier statement that the optimal strategy is for a 3rd base coach to send anyone with a chance of success greater than .71. After that, the net runs scored is a negative value and the tactic becomes counter-productive.

The value in the lower right of 240.7 represents an estimate of the additional runs all 30 major league teams would’ve scored in 2006 (using the notional set of data) if they all used an optimal baserunning strategy for balls hit to centerfield with runners on base. This comes out to 8 runs per team, which is not a lot. However, including balls hit to left and rightfield, the estimate grows to 26 runs per team (14% more balls are hit to left and right than to center). If one makes the assumption that runners are equally reluctant to try for an extra base with no baserunners in front of them (i.e. stretching singles into doubles, etc.), the estimate grows to 50 runs per team since approximately 47% of baserunning opportunities occur with nobody on base.

I concede that it’s quite a stretch to assume runners are reluctant to stretch hits at the same rate as they are in advancing on hits. Unfortunately, Retrosheet data doesn’t lend itself to the kind of analysis required to test that assumption. Regardless, one can safely say that “runner’s reluctance” could easily cost the average team 30-40 runs a year. This is significant. Using Bill James’ Pythagorean Theorem for run differential, it equates to 3-4 extra wins per season. Any team would love to have 3 or 4 extra wins. All it apparently takes is more aggressive baserunning.

At this point, it’s important to dispel a myth. The optimal strategy is not one where the actual results are equal to the break-even rate. Nothing could be farther from the truth. Viewing the table of notional data above, the optimal strategy has a success rate of .84, not the break-even value of .71. Including the initial 2006 data (97% success rate on 3500 attempts), the total success rate for an optimal strategy is somewhere around 92%. So the optimal strategy occurs neither where the red and purple lines intersect in the graphical chart above, nor where the blue and green lines intersect. Rather, the optimal strategy occurs where the slope of the blue line becomes parallel with the slope of the green line, which occurs about when the blue line crosses the 92% success rate for our notional data.

One could argue that this estimated optimal success rate of 92% is not so far removed from the actual success rate of 97%, and maybe runners and coaches aren’t wasting so many opportunities after all. I considered this possibility and rejected it because of the likelihood of miscalculations by the coach/runner along with calculated decisions to be more risk averse or accept more risk depending on the game situation. Allow me to illustrate with an example.

Suppose a 3rd base coach is faced with a series of baserunning decisions where the runners have a chance of success listed in the table below. The optimal strategy would look like this if the break-even rate is 71%.

The Optimal Strategy

Player     Chance of Success   Decision
Player A   100%                Send
Player B   90%                 Send
Player C   80%                 Send
Player D   70%                 Hold
Player E   60%                 Hold
Player F   50%                 Hold
Player G   40%                 Hold
Player H   30%                 Hold
Player I   20%                 Hold
Player J   10%                 Hold
Player K   0%                  Hold

The expected success rate for the data above with optimal decisions would be 90% (the average of 80%, 90% and 100%). However, sometimes the coach sends a runner when he shouldn’t, or holds a runner that he should send just because humans make mistakes. Similarly, late in a game when trailing by multiple runs, teams will play station-to-station baseball and take no risks at all. Likewise, trailing by one run, a team might take additional risks to try and score that tying run. Considering these factors, the actual results may look like this.

Possible Results with Mistakes and Risk Adjustments

Player     Chance of Success   Decision
Player A   100%                Send
Player B   90%                 Hold – Risk
Player C   80%                 Hold – Mistake
Player D   70%                 Hold
Player E   60%                 Send – Mistake
Player F   50%                 Send – Risk
Player G   40%                 Hold
Player H   30%                 Hold
Player I   20%                 Hold
Player J   10%                 Hold
Player K   0%                  Hold

Notice how the expected success rate under these conditions becomes 70% (the average of 50%, 60% and 100%). So even though the optimal strategy has a 90% success rate, the actual success rate could be considerably lower because of miscalculations and risk adjustments. That’s why I still believe the actual MLB success rate of 97% is an indication of extreme “runner’s reluctance” given that the break-even rate is 71%.

So far, this notional analysis has looked at all centerfield running situations from 2006 in aggregate. In reality there is a theoretical curve similar to the one above for every situation – every baserunner, every batting order, every ballpark, every pitcher, every defense, every inning, every out, every score, every…well you get the picture. There are literally millions of ways to slice a finite set of data.

Astute readers will recognize that the notional data used in this analysis is merely, well notional. The truth is that nobody knows what the actual curve looks like. For all we know, the curve has a steep drop-off similar to the worst case curve. The notional data was based on the assumption that each additional 1% of baserunners experienced a 1% lower success rate. If the rate was doubled and each 1% of baserunners resulted in a 2% lower success rate, the estimate of lost opportunity would essentially be cut in half. If, however, the success rate dropped at a slower rate, say half as quickly as the notional data, the run estimate would be twice as large. Although the shape of the curve and the magnitude of the lost opportunity may be mere estimates, we can be reasonably sure that there are some additional runs to be squeezed out of baserunning considering the large difference between a 97% actual success rate and the 71% break-even rate.

Now it’s up to MLB teams to use this information to their benefit. I would like to see them start sending more runners in an intelligent way. Third base coaches should have the break-even rates in their back pocket and refer to them in between pitches in anticipation of possible baserunning decisions. Teams should spend some off-season time doing video analysis of their ballplayers to determine success probabilities for each player in various situations. Likewise, teams should thoroughly scout opposing outfielders’ arm strength and accuracy to estimate probability adjustments depending on who fields the ball and where it’s fielded.

For decades, baseball has analyzed and timed the stolen base attempt to the nth degree - from the pitcher’s time to the plate, the catcher’s time to release, to the length of lead by the runner and number of steps and time to 2nd base. I’m not aware of any similar effort for other baserunning situations. With MLB victories worth million of dollars, now is the time to start putting emphasis on this long-neglected area, and correct the problem known as “runner’s reluctance.”

Ross Roley is a lifelong baseball fan, a baseball analysis hobbyist, and former Professor of Mathematics at the U.S. Air Force Academy.