I didn't have much planned today, but I was playing around with these conditional probability plots this week, and thought I'd share them. Conditional probability charts show the probability of an event happening, given one condition. In this case, they show the chance of a ball in play being hit on the ground given the height it crossed home plate.

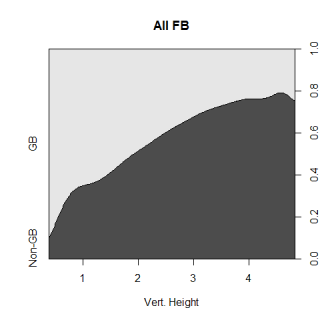
The graph below shows the probability of a fastball (that is put in play) either being hit in the air or the ground, given the vertical height where it crossed the plate. The dark gray region is the probability of the ball being hit in the air, while the lighter region is the corresponding chance of the ball being hit on the ground. The curve is smoothed slightly and the general pattern of low pitches producing more groundballs is what you would expect. This isn't surprising, but what’s cool is that you can see the continuous relationship between height and the chance of a groundball.

Moving on, the graph below on the left shows the same thing as the graph above (the chance of a random pitch to be hit in the air or on the ground), but only for fastballs with a pfx_z value of less than 5 inches. This means that the pitch ended up 5 inches higher than a non-spinning pitch would have, and while that value doesn’t mean anything by itself, that’s the cutoff point I used to define sinking fastballs. The graph below on the right is for all fastballs with a pfx_z value greater than or equal to 5 inches and just looking at the two graphs, you can tell that there is a big difference in the chance of a sinker being turned into a groundball compared to a regular fastball.

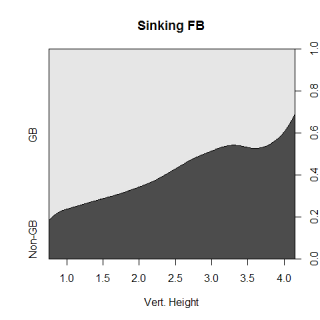
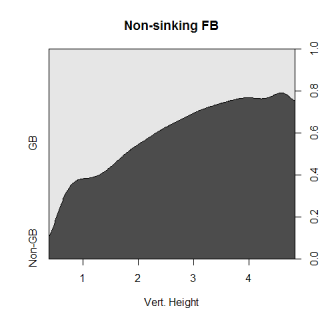
Very roughly, the strike zone goes from a height of 2 feet to 4 feet, so a sinker at the knees that is put in play has a 65% chance of being a groundball, while a non-sinking fastball at the same spot has a 45% chance to be a grounder if it is put in play. At the top of the strike zone, a sinker has a 40% chance of being a grounder, while a regular, non-sinking fastball has only a 25% chance, so a sinker up in the zone is almost as likely to get a grounder as a regular fastball at the knees. At almost every height, sinkers are 15-20% more likely to be hit on the ground than a regular fastball. There are a ton of other considerations to take into account if you were finding the true chance of a ball-in-play being a grounder, like the horizontal position of the ball and exactly how much a pitch "sinks" (or breaks or spins or whatever you call it), but this is just another illustration of why sinkers can be so valuable for a pitcher.

====================================================================

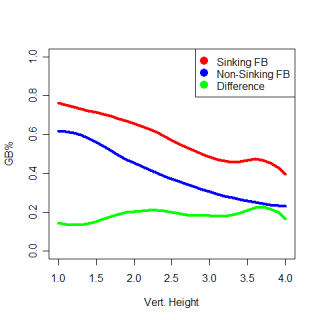
11/24 UPADATE: The 2nd and 3rd graphs I showed aren't very easy to understand, so here is a much more straightforward version of the information.