
| F/X Visualizations | April 24, 2009 |
Over at Beyond the Box Score Sky Kalkman posted an introduction to understanding pitchf/x graphics. It is a great post for people who are having a hard time understanding these graphics. I also liked the comments section where there is some discussion of the state of pitchf/x analysis. In particular some commenters noted areas of the current analysis they found lacking.
Trey Hilman's Chin commented:
I do have one question to go along with all this. For any particular pitch, is there a range of movement that is generally recognized as “good” for that pitch classification? I am terrible at judging “stuff” simply by watching a pitch, but it would be nice to look at some of these charts and intuitively see that a particular pitch had a “nasty slider” tonight, etc.
Similarly, azruavatar wrote:
5 inches of break is absolutely meaningless to me in the context of a slider. I also question whether all 5 inches are created the same. Rivera’s cutter is notorious for late movement. If a pitch moves 5 inches over 20 feet compared to 5 inches over 60 feet that’s an incredible difference.
It seems that people are having the hardest time intuitively understanding pitch movement and putting an individual pitch's movement in perspective. Another commenter suggested Josh Kalk's two-part Anatomy of a League Average Pitcher series. The first broke down the league average fastball, sinker and cutter by presenting the frequency distribution of speed and movement for these pitches, and the second did so for off-speed and breaking pitches. These allow one to see if, say, a pitcher's curveball breaks more than the average curveball. But we are still left wondering if that additional movement makes the pitch any more successful. I will begin to address this question here for the breaking (and knuckling) pitches, and look at fastballs and changeups in a future post.
The pitchf/x system measures pitch movement in a number of ways but the two easiest to understand are the horizontal movement (pfx_x) and the vertical movement (pfx_z) of a pitch. Alan Nathan has a helpful description of the meaning behind these two values:
pfx_x,pfx_z: The deviation (in inches) of the pitch trajectory from a straight-line in the x (horizontal) and z (vertical) directions...[T]he effect of gravity has been removed from pfx_z, so that both parameters are the "break" of the pitch due to the Magnus force on a spinning baseball...[A positive value of pfx_x corresponds to] a deviation to the catcher's right and a negative value to the catcher's left. Similarly, a positive value of pfx_z is a pitch the drops less than it would from gravity alone (most pitches fall in this category), whereas a negative value is a pitch that drops more than from gravity alone (e.g., a "12-6" curveball).
So the movement of a pitch is the difference between where you would expect the pitch to end up as it crosses the plate based solely on its velocity, trajectory and gravity and where it actually ends up as it crosses the plate. This difference is broken up into its horizontal and vertical components. Then you can plot the horizontal and vertical movements of a number of pitches together in a scatter plot to see the movement of a particular pitch type or from a particular pitcher.
Curveballs
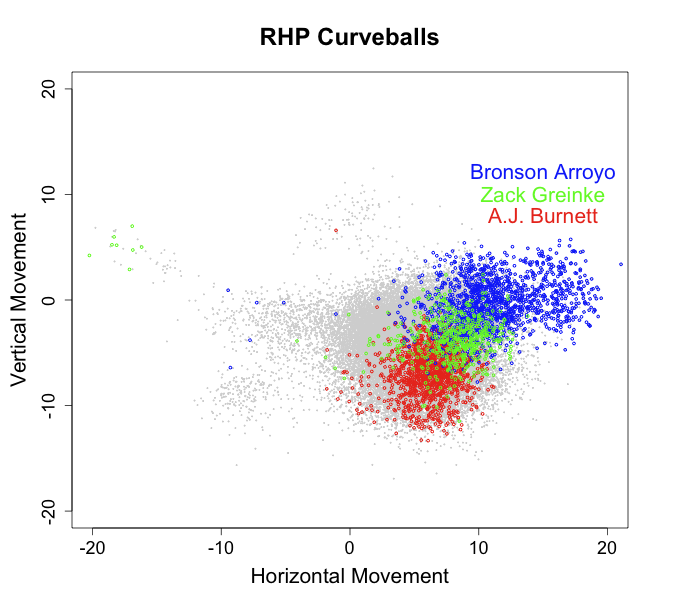
In gray, are all curveballs thrown by RHPs. You can see that most tail to the catcher's right by about 5 inches (meaning they tail away from RHBs) and break down by about 5 inches. On top I plotted the curveballs of three pitchers with distinctive and successful curves. Bronson Arroyo's curve has almost no vertical movement, but far and away the most horizontal movement of any curveball in the game. A.J. Burnett's curve, on the other hand, has some of the most downward movement of any pitcher's curve, but average horizontal movement. (Arroyo's curve's dependence on its heavy horizontal movement compared to Burnett's on its heavy vertical movement may partially explain Arroyo's more extreme platoon split compared to Brunett's). Zack Greinke combines intermediate levels of horizontal and vertical movement in his very successful curveball.
I am using the pitchf/x given pitch classifications and you can see three strange 'blobs' off of the central cluster of pitches. These are not curveballs. I think they are misclassified changeups. One cluster comes from sidearm pitchers and another from pitchers who throw sinking fastballs and changeups.
Now that we have seen the range of movement for all and a select group of individual pitchers's curves we can look at how curveball success varies by movement. In the images below I show the run value of a curve based on its movement. I decided to take a slightly different approach from my run value by location heat maps. I wanted to show not only the run value by movement, but also roughly the number of pitches with that movement. So I plotted the heat map colors on top of the scatter plot of pitches. Note that I change the color scale in each image, while this makes it harder to compare across images, it makes it easier to highlight differences within a particular image.
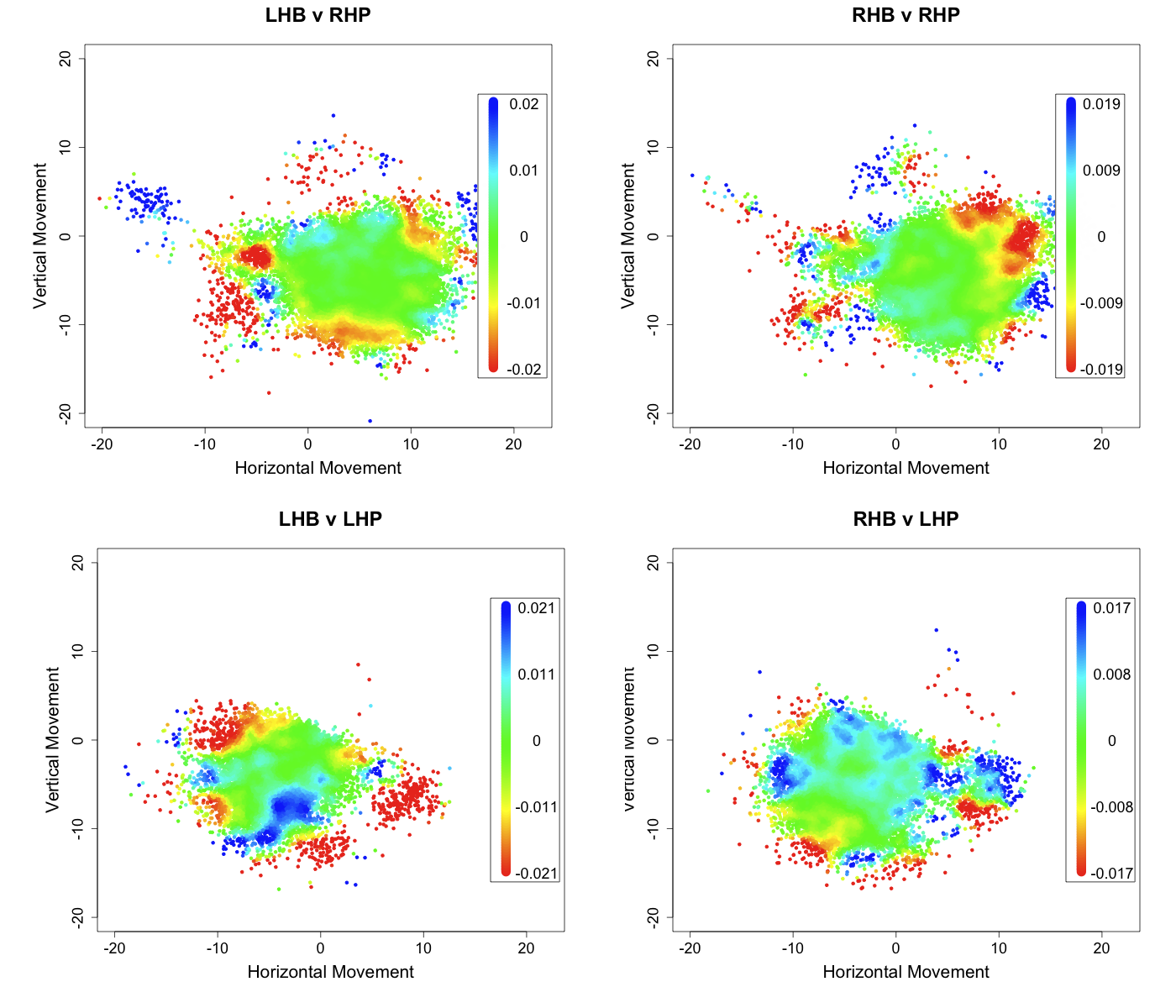
These are pretty messy complicated images. Studes suggests that at times these heat maps are too messy to be very informative. I think that is the case here (although I cannot agree too much or I lose my raison d'être). So I took a more traditional route below and plotted run value versus first the vertical movement (averaging over the horizontal) and then against the horizontal movement (averaging over the vertical).
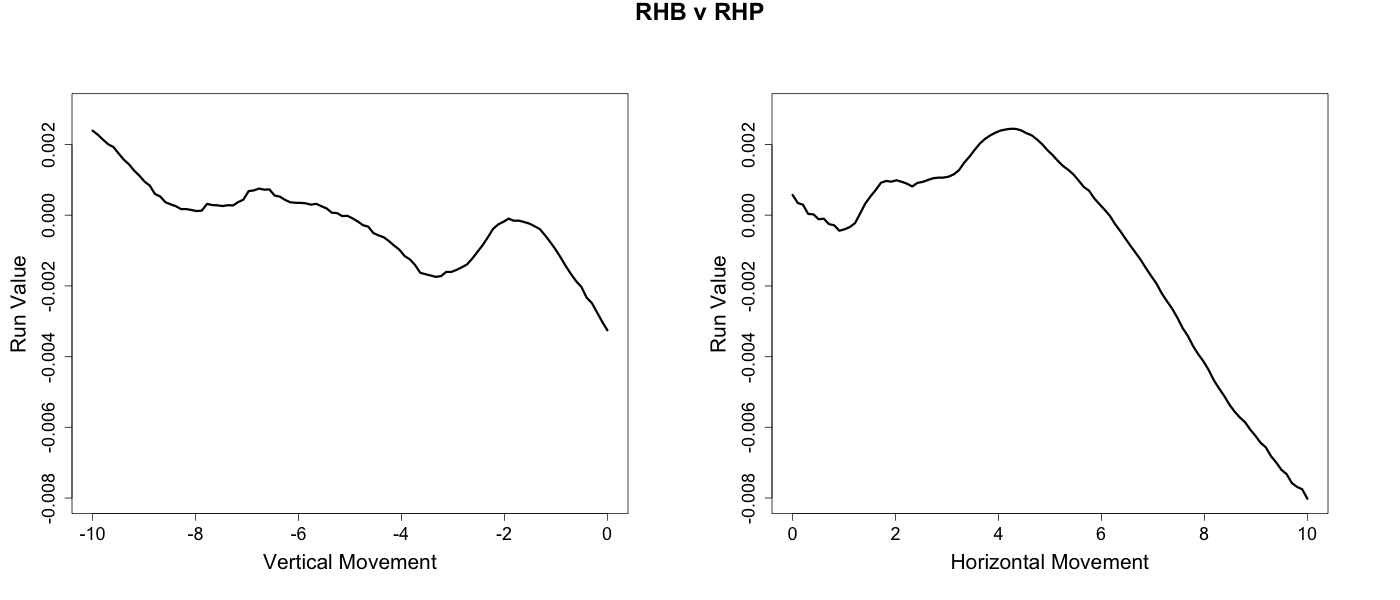
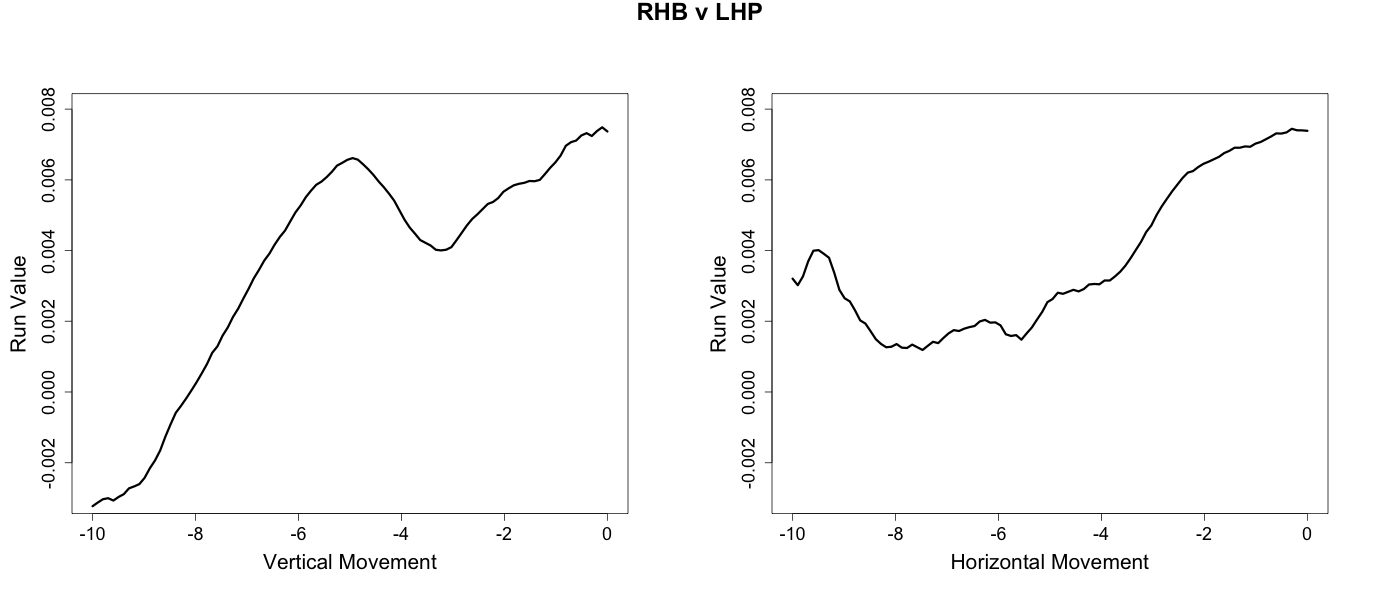
These figures reveal an interesting dichotomy between same handed versus opposite handed at-bats. In opposite handed at-bats the success of the curveball is mostly determined by its vertical break. The greater the downward break the more successful the curve. Conversely, in same handed at-bats the horizontal movement of the pitch largely drives the pattern. The more a curveball tails away from a batter the more successful it is.
Sliders

RHP's sliders, on average, have slight tailing away movement from RHBs and slight rising movement, although there is considerable variation. Greg Maddux's slider, for example, tailed in to RHBs. Justin Duchscherer's slider has little horizontal movement but above average rising movement. Carlos Marmol's slider is in the top five among sliders for both horizontal and downward movement, which makes it the slider with the most overall movement in the game.
I use the same technique described above for curveballs to produce the run value by movement images for sliders below. Since sliders are thrown overwhelmingly in same handed at-bats I only present those.
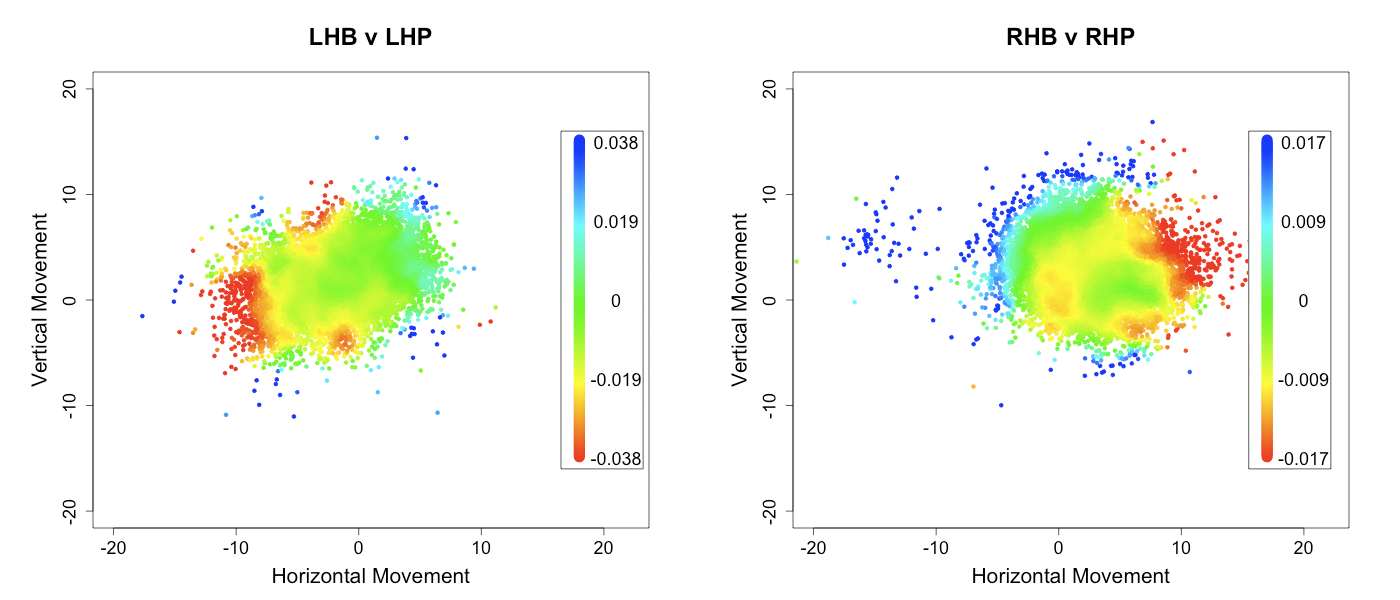
Here, I think, the heat maps show a relatively clear gradient, with sliders that tail away from the hitter the most being the most successful.
Knuckleballs
There are fewer knuckleballs thrown than sliders or curves, but I really wanted to include them. John Walsh wrote the seminal pitchf/x article on the knuckleball. He found that, unlike other pitches, knuckleballs do not have a consistent pattern of movement, but a random horizontal and vertical movement each anywhere from -15 to 15 inches (for Wakefield, at least). The success of an individual knuckleball varies directly with its, seemingly random, amount of movement; batters make less and poorer contact the more movement a knuckleball has. Using the method described above I am able to make one slight addition to Walsh's conclusion.
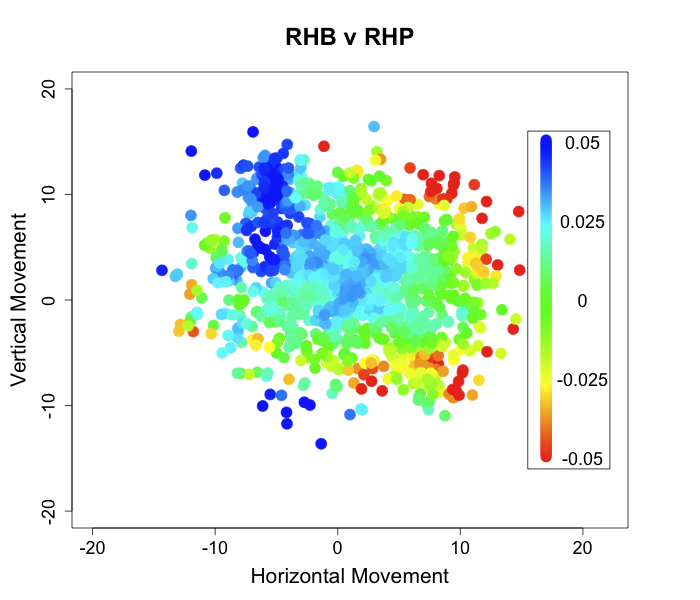
Outside of the north-west quadrant we get a confirmation of Walsh's results; there is a lower run value as the break increases. But knuckeballs with positive vertical movement and negative horizontal movement have even higher run values than those with no movement. Thus knuckleballs that break up and in to batters, even if they have a lot of movement, are very unsuccessful. This makes knuckleballs even more random; even if a pitcher can get lots of movement on his knuckleball if it happens to break up and in he could be in trouble.
In a future post I will look at fastball and changeup movement.
Comments
Great article, Dave.
I like your additional insight on the knuckler. That northwest quadrant is exactly where a typical RHP fastball moves, so a knuckler that breaks that way looks exactly like a BP fastball. No wonder they cream it.
BTW, I would like to take the credit, but that two-part Anatomy series was by Josh Kalk.
I'm looking forward to results on fastballs and changeups.
Posted by: John Walsh at April 24, 2009 7:01 AM
John,
Opps. I had it thoroughly in my head that you wrote those. I changed it. Thanks for bringing it to my attention.
Posted by: Dave Allen at April 24, 2009 7:35 AM
RJ's cool, too, but I, er Sky Kalkman, wrote that BtB Understand Pitch F/X Graphs article.
I agree heat maps can sometimes have too much going on, but that's also a good thing. For example, if you just look at horizontal movement or vertical movement alone, you're missing any dependence issues -- curve balls that don't move in one direction likely move more in another direction. I'm guessing that's what causes the humps in the one-dimensional graphs. That, and how similar/different the curve looks to other pitches in the repertoire.
Also, curve ball speed could play a large part in this analysis. Movement from spin is only part of why curve balls move. The other is that they're also a change up. And of course some pitchers throw a power curve which won't actually move as much in real terms as a slower curve with the same amount of spin.
Posted by: Sky's Biggest Fan at April 24, 2009 8:45 AM
Dave,
I really like this post. The dual use of heat maps and the more traditional plots is great. And don't worry, I think it would be very difficult for you to lose your 'raison d'être'!
Posted by: snowball2 at April 24, 2009 8:52 AM
Sky, er Sky's Biggest Fan,
Gosh, I am misattributing left and right here. Thanks for bringing that one to my attention. I changed it too.
I think that you are very right that pitch speed plays a big role too. Looking at just movement and averaging over speed and location is definitely very limited. If fast pitches, or pitches in the certain parts of the zone, are more likely to have a certain type of movement then those pitches will have lower run values. Here I will attribute that to movement while it is probably just a result of speed. So ultimately it will be important to look at speed and movement together.
Posted by: Dave Allen at April 24, 2009 5:11 PM
Great stuff. I like that you can see that average pitch movements often have positive run values, presumably because the batter is adjusted to them. In other words, below average movement is often better than average movement.
There is a distinctive green island in the RHB vs. RHP sliders heat chart for where slider movement is around average. And as you said for curveballs, same-handed at bats are driven by horizontal movement, where average is not average at all but actually in the hitter's favor, and same with opposite-handed matchups and vertical movement. I'm most interested in seeing how this relates to sinking/rising fastballs. I suspect that fastballs with average movement, which are called flat, get hammered.
Posted by: Jeremy Greenhouse at April 25, 2009 2:09 AM
Jeremy,
that is a good insight about pitches with average movement, which I didn't fully realize as I was writing the article. Thanks for bringing it up.
Posted by: Dave Allen at April 26, 2009 4:53 AM
Bert Blylevn should be in the hall of fame for his contributions to baseball. He was a great pitcher, and he is the best announcer I.ve ever heard, he is humerous, nand above all he is very intelligent of the game. Listening to Berts commentary has always been knowledgable and informative to me. He has always allowed me to capture my interest in the game. He was always a spectacular pitcher with his curve ball, and his domination of the hitter.
Posted by: Steve Taylor at April 29, 2009 7:05 PM
This is a fantastic article that basically proves what pitchers have known instinctively for 50 years.
In practice, when you swing at a ball breaking away from you, all of that horizontal break is lost power from your swing. Imagine getting punched in the shoulder by your big brother after you've made a snarky comment about his favorite baseball player: if you're moving away from the punch, even just a little, you end up absorbing most of the blow. If you tense up, you'll end up with a bruise.
So the more a slider or curve breaks away from the bat, even on good contact, it loses power and is more likely to be popped up to an outfielder or grounded.
The small movement thing was particularly interesting. I think the effect you're seeing is that on small movement, a hitter doesn't realize there was break on the ball until too late. Even the wiliest veteran's eyes will turn into a saucers as a fat, immobile curve, but when that sucker all of a sudden breaks with life, all of your power hits the top of the ball and you end up with a grounder.
A mid-level break, however, that ends up over the plate can get recognized. Hitters are taught to put a little wristed loop in their swings when they see it's a curve rather than a fastball coming. The loop won't help you on a big break, but if it breaks over the sweet spot you end up popping that little sphere of cork, twine and leather into a power alley, or, for the big guys, over the fence.
Posted by: Misopogon at April 30, 2009 2:07 PM