Last week I took my first look at the HITf/x data examining how the location of a pitch influences the speed of the ball off the bat and vertical angle of a resulting hit. In this post I am going to do the same for the horizontal (or spray) angle of the resulting hit. This is the angle of a batted ball into the field. Sportsvision reports this angle with 45° corresponding to the 1st base line, 90° straight up the middle (2nd base and center field) and 135° the 3rd baseline. Based on the discussion here it seems others find a -45/0/45 orientation more intuitive. So here I shifted to that orientation so 45° is the first base line, 0° straight up the middle and -45° the third baseline.

Max Marchi already looked at this topic using the GameDay hit location to determine the horizontal angle of the ball in play. He examined the tendency of hitters to pull inside pitches and go the other way with outside pitches. He also looked at the possibility of defensive realignment based on a given hitter's spray chart. Here I am going to look at the first topic and ignore the second which led to an, at times, heated discussion over at the Inside the Book blog.

In Max's work he looked at how much individual hitters pulled the ball based on the pitch location. Here I am going to average over all hitters to find a baseline. Below I show the horizontal angle of a batted ball based on the location of the pitch. Remember that negative angles correspond to to the left side of the field and positive to the right. In this case I chose a red-to-blue color scheme to high-light the difference between pulled and opposite field balls in play. I also flip the colors between RHBs and LHBs so that red is always pulled and blue opposite field. Like always the images are from the catcher's perspective.

Horizontal angle by pitch location

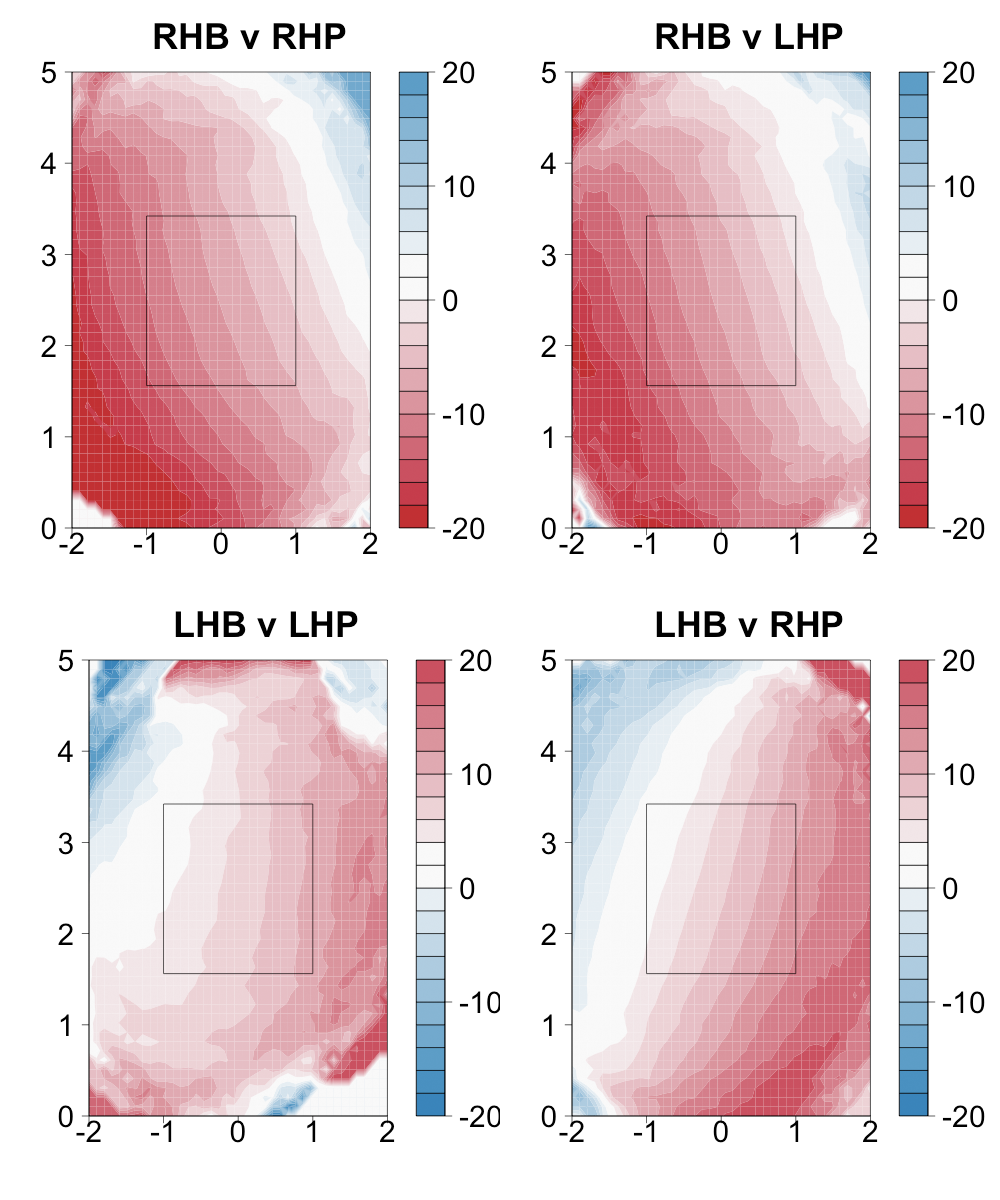
As expected inside pitches result in the furthest pulled balls and it is not until you get to the outside edge of the strike zone that the average ball in play is to the opposite field. So batters have a tendency to pull the ball, with a pitch down the middle on average being hit to about 5° to the pull side. In addition there is a slight trend for pitches low in the zone to be pulled more. It looks like RHBs pull the ball more than LHBs.

Horizontal angle by pitch location for ground balls versus balls in air

I was also interested in how strongly ground balls are pulled compared to balls in the air (fly balls, pop ups and line drives). Conventional wisdom is that ground balls are pulled more, as evidenced by the infield shifts that hitters like David Ortiz experience. In addition, Matt Lentzner set up a simple bat-ball collision model that predicted most ground balls go to the pull side and more balls in the air to the opposite field side.

So we have conventional wisdom and theory telling us what to expect, let's see what the data say. I redid the above analysis first with ground balls and then balls in the air. Instead of using the GameDay classification for GB versus LD or FB, I used the HITf/x vertical angle. Based on Harry Pavlidis' work here it looks like 7° is a rough cutoff between a ground ball and a ball in the air. So that is how I separated the batted balls.

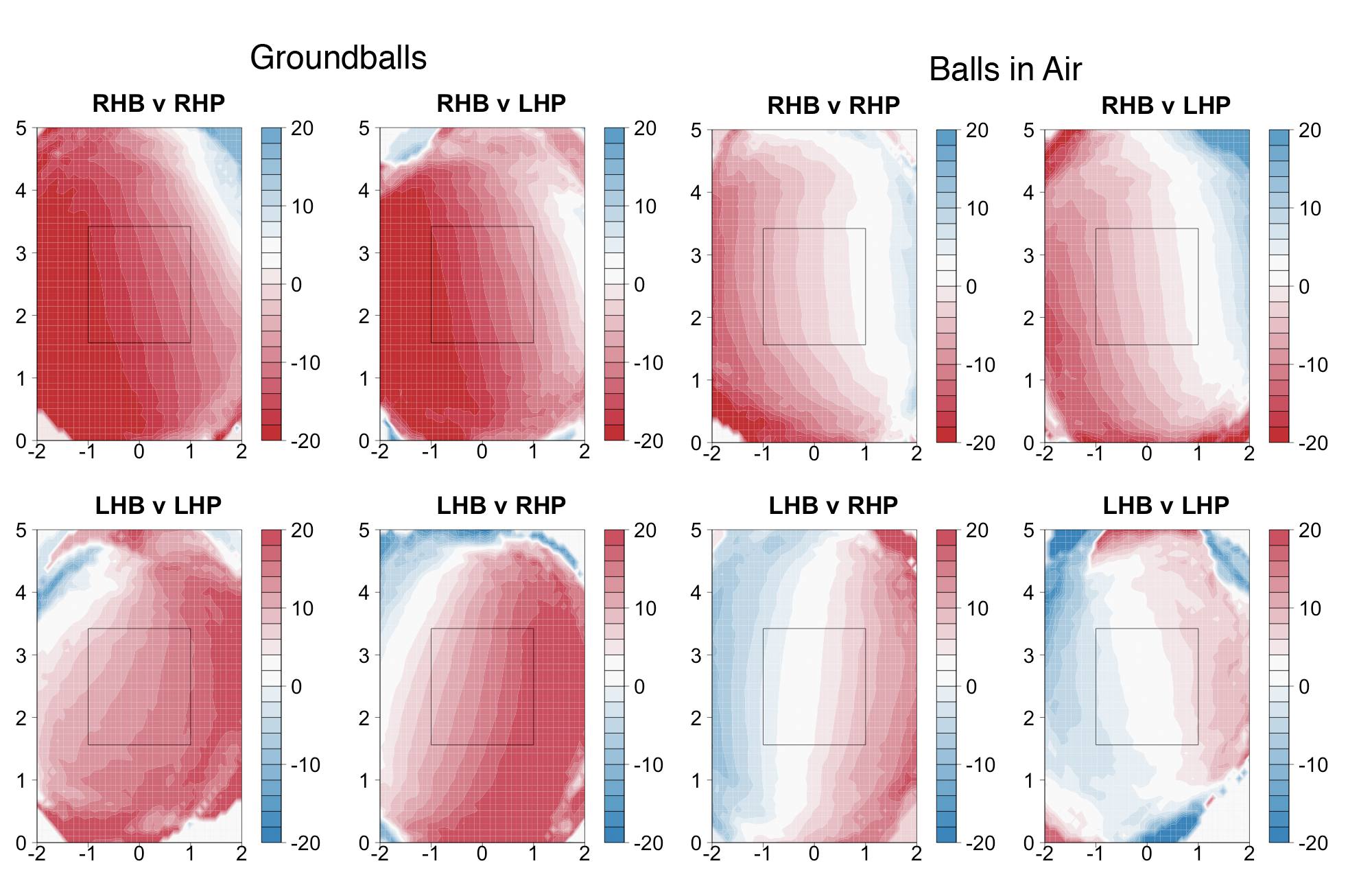
Just as expected ground balls go to the pull side much more often than balls in the air. For about the inside two thirds of the plate the average ground balls goes at least 10° to the pull side. Again RHBs show a stronger tendency to hit to the pull field. This could be because infield hits are more likely to the left side of the infield than to the right, so RHBs have an incentive to pull ground balls while LHBs have an incentive to go the other way with ground balls.

Fly balls, pop ups, and line drives have a much smaller tendency to be pulled and again it is weaker in LHBs. In fact there is almost no pull trend for LHBs on balls in the air; they tend to pull inside pitches and go the other way with outside ones.

Speed of ball off bat by horizontal angle

Finally I was interested in how much additional power a pulled ball has than one hit the other way. Mike Fast showed that pulled balls are more likely to be home runes, more likely to be line drives and have higher BABIP than opposite field balls in play. In fact, Mike showed, a pulled fly ball is ten times more likely to a home rune than an opposite field fly ball. I wanted to see the difference in speed off the bat responsible for this huge effect. Here is the horizontal speed of the ball off the bat by horizontal angle for LHBs and RHBs.

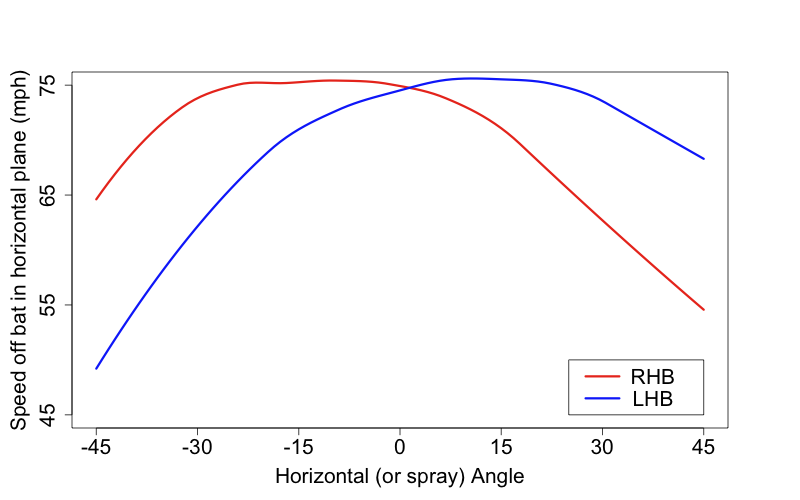
Batted ball horizontal speed reaches a maximum roughly between 5 and 25 degrees to the pull direction. Pulled balls are roughly 10 to 20 mph faster than those hit in the same angle to the opposite field.

Of course all of this analysis averages over all hitters. We know there are hitters who are assumed to be 'dead-pull' hitters or those with power to all fields. The data are now there, in a small sample with more coming, to examine these classifications. Do such hitting syndromes exist? How consistent are they for an individual hitter year to year? How does it impact a hitter's performance? It will be very interesting when enough HITf/x data become available to look at individual hitters at this level.