
| Behind the Scoreboard | June 23, 2009 |
Last week I provided a model for the expected value of Wins Above Replacement (WAR) for a particular draft pick in the MLB amateur draft. The model showed the top pick having an expected lifetime WAR of about 20, dropping quickly to about 6 WAR for the number 10 overall pick, and leveling to about 2 WAR for the #100 pick. The model also backed the conclusion that college players and hitters had higher expected WAR than other types of players.
Some readers suggested looking only at players' pre-free agency WAR to make the model more useful to major league teams. Others suggested that the advantage of college players over high schoolers has decreased over time. Still others wanted to see not only the expected value of a player's WAR, but the distribution of WAR's surrounding each pick. In this article, I intend to examine these suggestions and ideas to help provide a better understanding of the value of these draft picks.
Before I get started, I should say that I improved the quality of the data I was working with. I now have picks 1-50, every 5th pick until #100, every 10th pick until #500, and every 25th pick up to #1000 in my database. I also now have Sean Smith's full WAR database used to calculate WAR.
A Player's First 6 Years
First, as Tom Tango suggested, it's more useful to major league teams to have data on a player's first 6 years of WAR, rather than their career WAR, since the benefit of selecting a good player in the draft only lasts until they reach free-agency, after which a team must pay market value like everybody else. Here I fit the model using only the first 6 year WAR as the dependent variable (a year of service was defined as 130 AB, 20 games pitched, or 50 innings pitched in a season). As you might suspect, the data follows the same form and shape of the career WAR data. As it turns out, a player's pre-free agency WAR is almost exactly half of their career WAR. Both models are listed below:
Expected Career WAR = (21.67 + (-11.7 * pitcher) + (6.1 * college)) * selection ^ (-.54)
Expected First 6 Year WAR = (10.9 + (-5.1 * pitcher) + (3.1 * college)) * selection ^ (-.52)
where pitcher is equal to 1 if a player is a pitcher, college is equal to 1 if he is a college player, and selection is equal to the # overall selection in the draft.
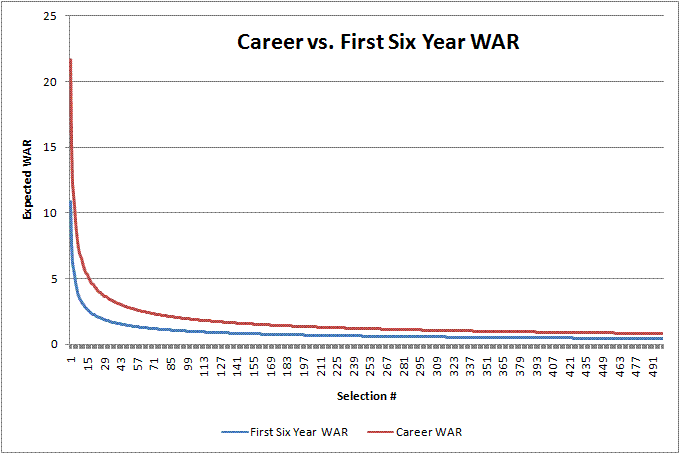
As you can see, the shape, determined by the exponent, is nearly the same in both models. Additionally, the scale parameter is about half of what it was in the career model, as are the bonuses and penalties for college players and pitchers respectively. While a player earns only a small percentage of his total earnings in his first 6 years, he earns half of his career value. Because the shape of the models are the same, this seems to be true for players on all levels of the draft spectrum.
Changes Over Time
Over time, the draft has evolved, along with teams' scouting methods and drafting strategies. One interesting thing to examine is whether the parameters in the model would change over time. Have teams started drafting more efficiently as time goes on? Have pitchers been better draft selections over time? How about college players?
I adjusted my model to include a parameter for year. Since the overall WAR for a draft must necessarily stay relatively constant throughout time, I also needed to add a year parameter in the exponent. The new model was of the form:
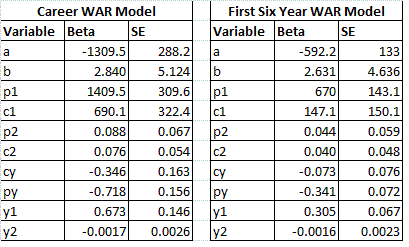
Expected WAR = (a + (p * pitcher) + (c * college) + (y1*year)) * selection ^ (b + y2*year)
The result of the model was a significant positive parameter for the y1 variable, but a corresponding negative y2 value (y2 was not significant in a test, but as I mentioned, if we include y1, y2 must also be included to maintain the proper balance). This indicates that teams are now drafting more efficiently - high picks have a higher WAR than in years past, while low picks have a lower WAR than in years past.
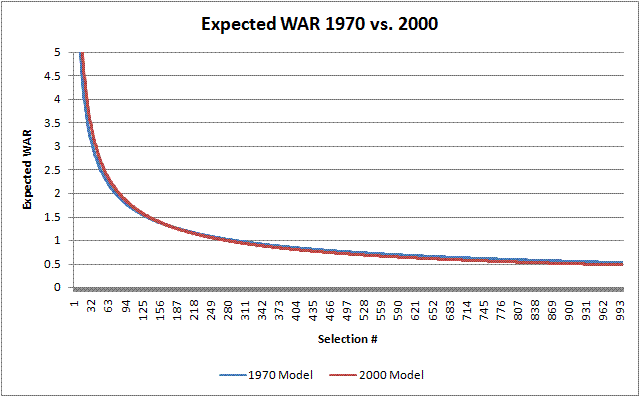
According to the model, #1 selections in the year 2000 expect to have a career WAR of 26.1 , while #1 selections in the year 1970 were expected to have a career WAR of 19.4. However, as the rounds go on, this advantage decreases until after approximately pick #200, after which the old picks are expected to do better than recent picks. Overall, the result is approximately the same total WAR for both modern and old drafts, but the early picks are more valuable in recent drafts than in years past.
This makes sense because scouting methods and statistical analysis have given teams more accurate prognosticating abilities about a player's future major league potential. With this increase in information, the better players are drafted sooner, clustering the WAR distribution more heavily in the early part of the draft. Below, is a zoomed in graph of 1970 vs. 2000 WAR by draft picks where you can see the lines cross.
It's also been hypothesized that the value of pitchers and college players has changed over time. To test whether this is true, I added interaction terms to account for this possibility. The model now takes the following form:
Expected WAR = (a + (p * pitcher) + (c * college) + (y1*year) + (py*year*pitcher) + (cy*year*college)) * selection ^ (b + y2*year + p2*pitcher + c2*college)
A reader had suggested that college players were more valuable in the past, but that this advantage no longer existed. The model finds some evidence of this claim - the cy variable is negative, indicating a decrease in the relative value of college players over the years. Another way of looking at this is that highly drafted high school players have increased their value more rapidly than college players over the years. For #1 selections, high school hitters are expected to gain 20 more WAR now than in 1970, while this advantage decreases to only 10 WAR for college hitters. This result is not significant for the first-six-year WAR model, but it is significant for the career WAR model.
The value of pitchers over time however, has decreased strongly. Despite the fact that #1 picks as a whole have much a much higher expected WAR now than in prior years, the expected WAR of a pitcher drafted overall #1 is actually less than it was in the early years of the draft. The is in stark contrast to the strong increases over time for #1 hitters. Whether this is the result of teams trying extra hard to build "pitching organizations" or is due to other reasons, it appears highly drafting pitchers is an even riskier proposition today than when the draft began.
Below is a table of the two full models in determining the expected WAR by draft position.
Distribution of WAR by Pick
Also interesting is not only the expected WAR for each pick, but the probability of becoming a certain caliber player. Using a model of the logistic form, I estimated the probabilities of gaining a certain level of WAR. The model was of the form:
P(WAR) = exp((a+p1*pitcher+c1*college)*selection^(b)+int)/(exp((a+p1*pitcher+c1*college)*selection^(b) + int) + 1)
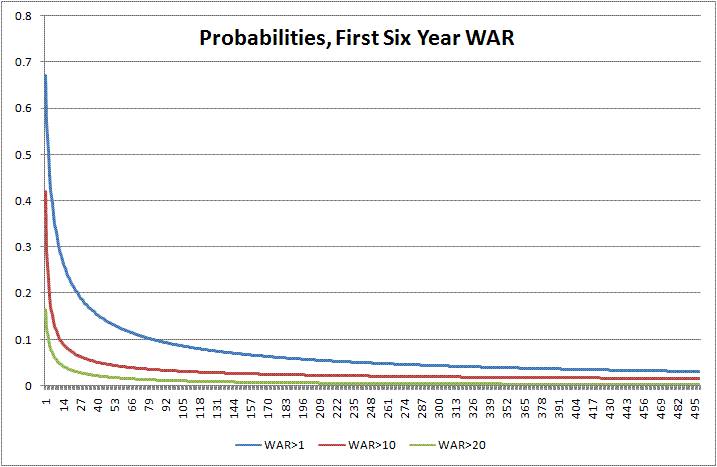
The models often had troubled converging, so the year terms and the exponential terms for pitchers and hitters were left out of the model. However, you can expect that they would have the same pattern as the models based on the expected value of WAR. Below you can see a graph of the probabilities of hitting various career WAR cutoff values, based on the above model. The graphs are for high school hitters.
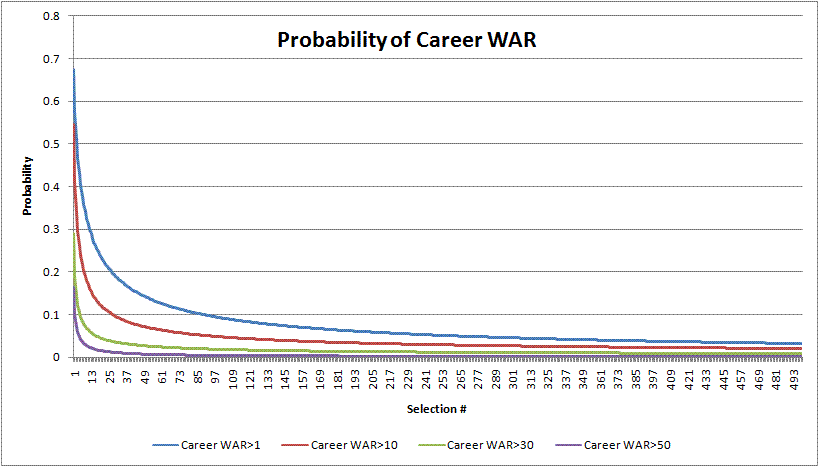
As you can see the #1 overall selection has about a 2 in 3 chance of making a positive impact on a major league club. The probability for a decent impact of 10 WAR is 54%. The probability of a 30 WAR career, which is a career which probably includes a couple of All-Star appearances and several solid seasons is 29%. The probability of a 50 WAR career, which is close to that of a borderline Hall of Famer, is about 16%. Overall, there is a fair chance that a number one selection will never make an impact, but also a non-trivial probability that he will end up in the Hall of Fame. This indicates the obvious large variability in a player's potential career.
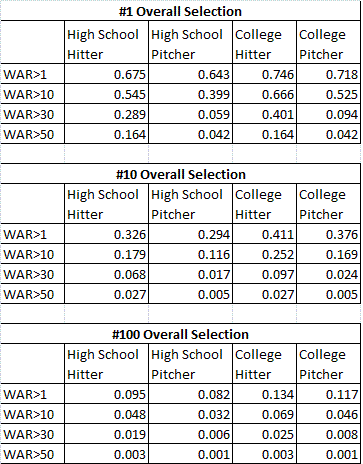
The chart above shows the model outcomes broken down by type of player and pick. One interesting finding is that pitchers are about as likely as hitters to make a positive impact on the major leagues with WAR>1. However, they start to slip when measuring the probability of having a great career. A college pitcher actually has a greater chance than a high school hitter of having a WAR>1 (71% vs. 68% for the #1 pick). However, the odds of having a WAR>30 are very much in the hitter's favor (9% vs. 29% for the #1 pick). While teams appear just as likely to get their pitching prospects to the majors, the probability of having a great career is quite small, even for top picks. This is the driving force behind the reasoning that teams should take hitters over pitchers in the draft.
For those more interested in players' pre-free agency WAR, below is a graph of this result, which largely follows the same shape as well as the same college/pitcher tendencies.
Conclusion
In conclusion, the following things can be said:
1) The first few draft picks are worth vastly more than later picks - a fact that is becoming more and more true as time goes by.
2) College players are a better bet than high school players, although this advantage has decreased through the years.
3) Pitchers, on the other hand, are less likely to bring value, a fact that is more true today than it was years ago.
4) Finally, highly drafted pitchers are about as likely as hitters to make a positive impact in the majors, but are much less likely to be truly great players.
I hope this study brings a greater understanding and insight into the value of draft picks and what type of player is likely to contribute at the major league level.
Comments
Sky: Excellent research and presentation. I agree with the conclusions as well as the reasons behind them, especially the increased efficiency in scouting and drafting strategies. The better players are now being drafted early, which also means there are fewer opportunities to select overlooked prospects like in the earlier days of the draft.
Posted by: Rich Lederer at June 23, 2009 8:32 AM
Changing the axes... making one or both logarithmic could help with the presentation a bit and maybe help see any more interesting details.
Also, would show more of the difference between 2000 and 1970.
Posted by: AMR at June 23, 2009 11:12 AM
That was a fine piece of research, Sky. What do you think of changing the rule that prohibits teams from trading draft picks?
Posted by: Al Doyle at June 23, 2009 12:05 PM
Great stuff. I am not clear on why conclusions 3 and 4 would be true, besides statistically. What are teams doing differently there or how are the guys who get drafted different than they used to be? Maybe you say it above but I missed it
Posted by: Cyril Morong at June 23, 2009 6:20 PM
Thanks for the nice comments. Cyril, I #3 indicates that pitchers are overvalued - perhaps teams feel more pressure now to build pitching from within. #4 indicates that it's tough to predict the great pitchers from the mediocre ones. A blazing fastball will probably get you to the big leagues, but it takes a lot of other intangibles to be one of the all-time greats. That's my take at least.
Al, in theory I'd like to see teams be able to trade picks, but I'd be worried that the good teams could essentially buy the best draft picks, thereby increasing their monopoly on talent. If they allow it, I'd be interested to see if that comes true.
Posted by: Sky Andrecheck at June 25, 2009 7:11 PM
Sky
Thanks
Cy
Posted by: Cyril Morong at June 26, 2009 7:19 PM