
| February 26, 2010 |
I have talked about before how I think that pitch sequencing analysis is one of the big places that pitchf/x data can be useful. I know that I linked them in my last post, but I want to again highlight just some of the great work done so far on the topic: Joe Sheehan looked at the frequencies of pitch types following each other for a handful of pitchers; Josh Kalk had a couple of articles one looking at the topic generally and another looking at the high fastball then curve combination; Max Marchi looked at the best one-two pitch combinations; and Jonathan Hale looked at the effect of fastball speed on subsequent changeups.
As I noted in my last post on the topic, about Mariano Rivera, for me the best way to start this study of pitch sequencing is to find simple, easy-to-analyze examples. Last time I choose Rivera since he has effectively three pitches, an inside cutter, an outside cutter and a fastball. This makes the analysis of pitch sequencing relatively straightforward. Today I am going to take a similar approach but broaden the scope of pitchers.
To do so I choose a group of pitchers who have a simple pitch repertoire. I choose fastball-sliders relievers. There is a rather large group of relievers who succeed with just the two pitches so it offered a large enough sample size of pitchers with just two pitches. Arbitrarily I picked out all relievers who in 2009 threw 90% or more fastballs and sliders and threw at least 30% of both of those two (so I didn't just get guys who went up and threw all fastballs). So when a batter faces one of these guys he knows he is going to see a fair number of fastballs and sliders, but not much else. To further simplify the analysis I just looked at at-bats between RHPs and RHBs.
As a group these pitchers threw 53% fastballs, 44% sliders and 3% other pitches in 2009. Here is where those pitches ended up in the strike zone, again just pitches to RHBs.
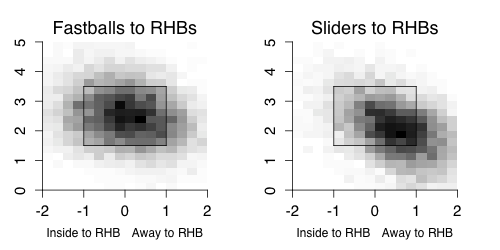
Not surprisingly the fastballs mostly around the zone and the sliders down-and-away. That is just for reference, the main point of the post is the sequencing aspects of the pitches.
First we can see whether these pitchers were more or less likely to throw a slider, or fastball, based on the previous pitch. For each pitcher I looked at the fraction of sliders after a fastball or after a slider versus his overall fraction of sliders. The same for his fastballs.
Situational slider fraction compared to overall slider fraction after slider 1.17 after fastball 0.95 Situational fastball fraction compared to overall fastball fraction after slider 0.88 after fastball 1.06
It looks like pitchers return to the same pitch more often than switch. I am not sure whether this has to do with batter quality (low-power batters are more likely to see fastballs which result in more fastball-fastball combinations) or count (the pitch after a hitter’s count, when a fastball is likely, is still likely to be a hitter’s count) or whether these pitchers are truly preferentially going slider-slider and fastball-fastball.
For whatever reason it happens it turns out to be a good idea. Here I note the difference in average run value of slider after a slider or fastball from the average run value on all sliders. A negative number means the pitch is better, gives up fewer runs, in that situation. For the rates, whiffs and slugging, I switch to fraction rather than difference.
sliders
rv100 whiff slg on contact
after slider -0.05 1.02 0.87
after fastball 0.43 0.95 1.16
fastballs
rv100 whiff slg on contact
after slider 0.02 1.01 1.08
after fastball -0.18 0.97 0.91
Sliders after a previous slider have better results than the average slider. This is seen in the whiff rate and in the slugging on contact. Similarity for fastballs there is better performance after a previous fastball, although it is seen just in the slugging on contact fastballs. So the whiff rate on a fastball following a fastball is a little lower than the average fastball, but the slugging rate is much lower. On the other hand both of these pitches are worse after the other compared to their average performance.
Maybe batters facing these two-pitch pitchers expect a slider after a fastball, and vice versa, and when they see the same one again it trips them up. Or again this could be some sort of sampling effect. Either way I hope to continue this analysis looking at the interaction of subsequent pitches based on their location and movement.
Comments
Dave,
Now that you've assigned values to these situations, can you say anything about whether they are choosing the sequences optimally?
I seem to recall that game theory and linear programming can determine optimal frequencies for choosing options in games played repeatedly. I feel like this framework might apply since the missing piece was the run valuation of the choices.
What are your thoughts? do pitchers throw the slider after the slider too often or too much?
Posted by: Bob at February 26, 2010 2:16 PM
Good stuff Dave. Like yourself, I love anything to do with pitch sequencing.
Just a quick question, were the rv100's shown a weighted delta of all pitcher's in your sample compared to their average slider/fastball rv100's, or just the actual numbers in your sample. I can understand if you didn't use the delta method, cause it's a bitch to code, but I'd just like some clarification.
I'm not surprised that fastballs are worse off after sliders than after fastballs. I know that Josh Kalk found that pitching backwards is generally a horrible strategy, and that is something that I have found myself as well looking at it in more detail. Actually, that seems like something that should be investigated further.
Can't wait for the next article!
Posted by: Nick Steiner at February 26, 2010 10:52 PM
Bob,
Great question. I don't really know that game theory mathematics very well. I think Chris Moore, another Baseball Analysts author, is more comfortable with it than I, so maybe he can address this.
Nick,
Yeah it is the delta method. At first I did it the second way, but that slider-slider combination would include more guys who threw a slider more often, and presumably had a good slider, than the slider-fastball grouping. Sorry that I was not clear about that in the text.
Posted by: Dave Allen at February 27, 2010 9:54 AM
Dave:
Fascinating stuff, as always. I'm having trouble making sense of the result for SL-FB. You report the rv100 is +0.43, quite a bit worse than a pitcher's average slider. However, this must represent about half (or more) of all sliders these pitchers throw. In order to be .43 runs worse than average, then the other sliders they throw must be far better than the average. Yet the SL-SL combo is -.05, very close to average. And since more than 90% of their pitches are SL or FB, there can't be enough other sequences to matter much. So I can't see how this all adds up. (I realize the two pools of pitchers are not the same, but since you're using the Delta method it doesn't seem like that should matter much.)
Posted by: Guy at February 28, 2010 1:27 PM
Oops, that should say "FB-SL" in 1st sentence.
Posted by: Guy at February 28, 2010 1:28 PM
Guy,
Yeah I am not sure what is up there. To begin with there are more slider then slider combos than fastball than slider combos, so that will account for some of the difference. So the average slider group will have more sliders after a slider than sliders after a fastball. In addition it could have to do with first pitch sliders, which are counted in the average slider group but in neither the slider after slider nor slider after fastball. Still as you point out the difference seems really big. I will go back and check it out.
Thanks for the comment.
Posted by: Dave Allen at March 1, 2010 7:31 PM