
| Touching Bases | May 25, 2010 |
Power vs. finesse. It's the classic debate. Spanning over 60 feet 6 inches, the difference between a 90 mile-per-hour fastball and a 95-MPH heater makes up a couple hundredths of a second. More importantly, those 5 MPH represent the difference between fringe stuff and an above-average Major League fastball. So how do pitchers compensate for shortcomings in velocity?
Throwing left handed is the simplest solution. The demand for southpaws is so great and the supply so scarce that the price for a lefty far surpasses that of an equally talented righty. Put another way, left-handed pitchers can accomplish more with less. So left-handed pitchers were excluded from my sample.
My sample consisted of of over 100,000 pitches from the past two calendar years. I grouped pitches by batter handedness as well as by velocity--depending on whether the velocity rounded off to 90 MPH or 95.
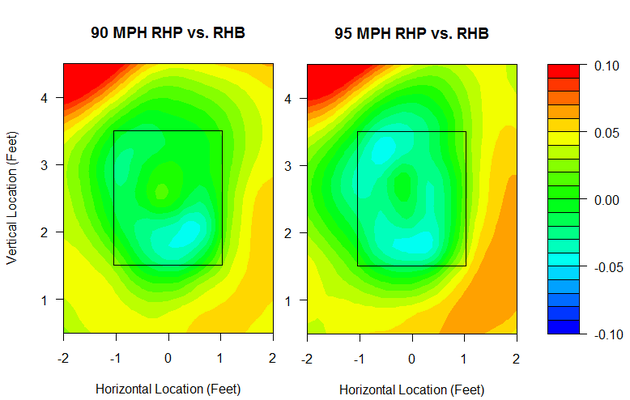
First, I looked at pitch location. The color scales that portray run value are the same for both images, so you can compare them directly.
Soft tossers can't survive by living up in the zone. A 90-MPH pitch can be thrown in the perfect spot in on the hands, and it still won't have the same success on average as a 95-MPH pitch that misses by half a foot. However, pitchers who throw 90 experience just as much success throwing down and away to same-handed batters as pitchers who throw 95. In this regard, pitch location can be a true equalizer. Joakim Soria locates his 90-MPH fastball so well that it's in the upper echelon of all fastballs, while Daniel Cabrera has located his 95 MPH fastballs so poorly that he's out of the league.
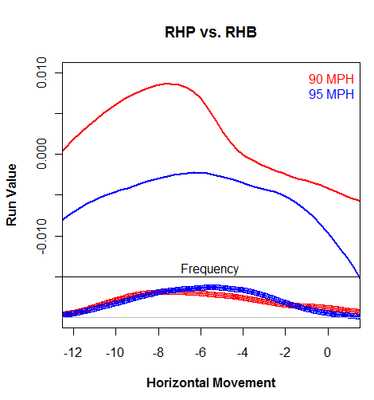
I also looked at pitch movement. The magnitude of the effect of pitch movement is much smaller than that of pitch location. Below, run value is plotted against horizontal movement in the solid-line portion of the graph, while a histogram for horizontal movement can be found at the bottom.
A 90-MPH pitch with average movement is a disaster. Even a 90-MPH pitch with great tail can't match an average 95-MPH pitch unless the 90-MPH pitch also has sink on it. But if a pitcher can really cut the ball so that it acts as a cutter, or even a slider for some, it can match an average 95-MPH fastball.
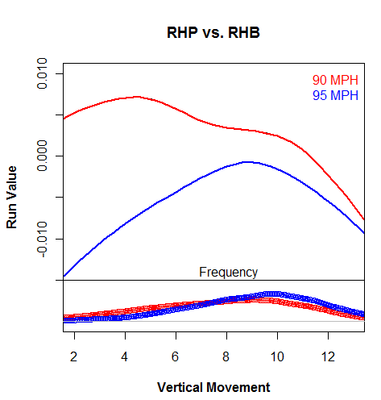
And vertical movement:
I find this to be an interesting trend. The 90-MPH pitchers are better off throwing rising fastballs, while 95-MPH pitchers are just as well off throwing sinkers or risers, so long as they stay out of that ten-inch danger zone to which the batter is accustomed.
In combining both horizontal and vertical movement, it's evident that Peter Moylan generates enough movement on his fastball to throw it at elite levels, while Cabrera, again, has a mediocre-to-awful fastball in spite of his velo. Remember, I'm only including 95 MPH pitches, so imagine how bad his fastball must have been in 2009 at 91 MPH. Cabrera is the poster boy for pitchers who can throw gas but have no command or movement, rendering their fastball ineffective. Kevin Jepsen, Jonathan Broxton, and Brian Wilson are examples of pitchers whose 90-MPH pitches are better than most pitchers' 95s, since those guys are throwing off speed at 90. Also of note: Jenrry Mejia's fastball has excellent movement.
Mixing location and movement into a regression, here are the best 90-MPH fastballs with at least 100 thrown:
Jared Burton
David Robertson
Peter Moylan
Ryan Franklin
Brian Sanches
Joakim Soria
Zack Greinke
Cory Wade
Roy Halladay
Mariano Rivera
David Robertson continues to be the man. No pitcher's 90-MPH fastball penetrates the top tenth of my sample, but all of these pitchers are squarely above average. They show that 90 MPH can beat 95, especially when the 95 is coming from the likes of:
Manny Acosta
Jason Bulger
Mitchell Boggs
Craig Hansen
Daniel Cabrera
Cabrera's 95 MPH fastball was the third worst fastball in my sample, and no other 95-MPH fastball fell in the bottom 40. The 90-MPH version of Cabrera's fastball was arguably better than his previous iteration.
Comments
Jeremy,
Fascinating. I am a bit confused as to your interpretation of the vertical movement vs. run value graph. Can you tell me where, exactly, I'm going wrong?
Here's my understanding: negative run values are better for the pitcher. A positive vertical movement value indicates sink.
If this were the case, it seems like the sinker is in fact a better pitch selection than a straightball for a 90 MPH right-hander.
Posted by: Peter at May 25, 2010 3:56 PM
Peter, Positive vertical movement indicates rise. Sorry I haven't been clear. From now on, I think I'll label my graphs with inside/outside, tail/cut and rise/sink.
Posted by: Jeremy Greenhouse at May 25, 2010 4:37 PM
Thanks, Jeremy.
BTW, how does that work. As in, what's the frame of reference. Obviously the fastball isn't actually rising twelve inches.
Posted by: Peter at May 25, 2010 11:33 PM
Right, but all fastballs are thrown with some level of backspin, which makes the pitch defy gravity to some extent. So while a theoretical spinless pitch would move zero inches, a fastball "rises" twelve inches, and even a sinker "rises" a few inches. Curveballs, and sometimes sliders, have enough topspin to achieve negative vertical movement as compared to a theoretical spinless pitch. Chris Young throws a true rising fastball at a similar velocity to Brandon Webb's true sinking fastball, and the difference in movement due to spin deflection is about 15 inches. Sidearmers and submariners throw fastballs with negative vertical movement, and in turn, their curveballs actually "rise" with positive vertical movement.
Posted by: Jeremy Greenhouse at May 25, 2010 11:53 PM
Jeremy's absolutely right. (and keeps knocking out the good articles!)
Another way that I like to think of it is that there are three forces acting on the ball: gravity, spin (Magnus), and drag. Those three together pretty much explain the observed movement of every pitch type.
Gravity causes every pitch to sink. It has longer to act on the pitches that are thrown slower, like curveballs and changeups, so it makes them drop more. It has less time to act on a fastball, so it makes it drop less.
As long as the pitch is spinning fairly fast, drag simply slows the pitch down by about 10% from release to plate. If the pitch is spinning very slowly, like a knuckleball, the drag force will act unevenly on the ball and make it curve unpredictably.
The spin force pushes a pitch with backspin up, a pitch with topspin down, and a pitch with sidespin to the opposite side.
A fastball has backspin and sidespin, so the spin force will push it up and make it tail. It doesn't push it up more than gravity is pulling it down, so the fastball still drops, but not as much as would without the backspin. A changeup also has backspin (though usually not as much as the fastball) and sidespin and will get pushed up and toward the pitcher's arm side, like the fastball. However, since gravity is the larger force and the changeup takes longer to get to the plate, it will drop more than the fastball. A slider usually has a little bit of sidespin and maybe a little topspin or backspin, but most of its spin is usually around the direction of travel, like a spiraling football, such that it doesn't apply any force to make the pitch break. The "break" of a typical slider's trajectory is mostly from gravity plus a small bit of spin force. A curveball has topspin that makes it drop even more than it would due to gravity alone and sidespin that makes it move toward the pitcher's glove side.
So that's a different way to say the same thing Jeremy did.
Posted by: Mike Fast at May 26, 2010 8:05 AM
Thanks for stopping by, Mike. Just curious, but I believe I've seen some analyst-probably you-say that they've never found a gyroball in PITCHf/x data, and I'd be interested to know what pfx_z value you think it might show.
Posted by: Jeremy Greenhouse at May 26, 2010 8:30 AM
Very helpful Jeremy and Mike. Thanks a lot.
Posted by: Peter at May 26, 2010 10:47 AM
Jeremy, one has to be careful about the definition for a gyroball. I've heard many conflicting things described as such.
For example, the Japanese shuuto seems to be the American two-seam or sinking fastball. The pitch Tezuka describes as having football spiral spin sounds like a slider on that basis, but then he says it has fastball speed. I'm skeptical until I see some evidence of how such a pitch would spin and move.
C.J. Wilson is the only MLB pitcher that I know to have claimed to throw the gyroball. He actually identified a couple specific instances where he threw it. In those instances, I couldn't tell any difference between that pitch and his regular fastball in the PITCHf/x data. The "spin-around-the-direction-of-travel" description is not consistent with the behavior of the pitches that Wilson threw and called gyroballs.
So either Wilson is not throwing the Tezuka gyroball, or the Tezuka gyroball doesn't do what Tezuka says it does in terms of spin and movement. Either of those seem possible to me. Or I suppose Wilson could have purposefully misled us or simply been mistaken about what he threw when. I doubt that, but I can't completely rule it out.
Posted by: Mike Fast at May 26, 2010 10:53 AM
Love this stuff but have one novice question: If home plate is 17" wide, why show a rough strike zone that's 24" wide? I understand the zone doesn't really matter since it's not "real," but it still bugs me a bit.
For example, the heat chart for 90s FBs reveals that not only is there a sweet spot on the hands, it's on the hands well inside the zone.
Posted by: Cory at May 26, 2010 12:43 PM
Cory, home plate is 17" wide, which means that the rulebook strike zone is 20" wide (plate + one radius of the baseball on either side).
In addition to that, the umpires tend to call strikes a few inches outside off the plate, so some analysts represent that by using a 24" wide zone.
I prefer to use the 20" zone and explain the extra strikes outside, but it ends up being confusing to somebody no matter what you do.
Posted by: Mike Fast at May 26, 2010 12:53 PM
Great stuff, as always, Jeremy! You're still not working for a team?
Posted by: MGL at May 26, 2010 7:14 PM
Mike, thanks again. One question, though: why not one diameter of the baseball on either side?
MGL, flattered again.
Posted by: Jeremy Greenhouse at May 26, 2010 10:25 PM
Jeremy, PITCHf/x tracks, or attempts to track, the middle of the baseball. If the middle of the baseball is 1.45" (one radius) off the edge of home plate, then the edge of the baseball just grazes the edge of the plate.
On a related note, it might be reasonable to argue that we should add a half inch or so for the random measurement error inherent in PITCHf/x and another inch or so for the typical systematic/calibration errors. However, these will average to near zero, so I don't typically include them in my definition of the zone, unless I'm talking about a single very borderline pitch.
Posted by: Mike Fast at May 27, 2010 8:03 AM
I've been looking for the answer to this question, hope you can help.
How many feet difference is there between a 90 mph fastball and an 80 mph fastball in relation to the pitcher and home plate? Or, when a 90 mph fastball reaches home plate, how far behind, approximately, is the 80 mph pitch (in feet)?
Thk you,
Rob
Posted by: Rob Cramer at June 8, 2010 7:43 AM