Last time I checked in, I looked at the percentages of fastballs thrown to different types of hitters based on the count. Toward the end of that article, I threatened to try to predict via regression when a pitcher would throw his fastball and this article is the preliminary result of that threat. What I wanted to do was find whether a pitcher threw a fastball or not, a binary variable, based on a particular list of factors, which was made up of both continuous and discrete variables. Regular linear regression can't handle binary dependent variables, but there is a special type of regression, logistic regression , that is designed for just this type of analysis. Given an dependent variable and one or more independent ones, a logistic regression will solve for the logarithm of the odds that a binary event is going to occur. Unlike linear regressions, where the relationship between the dependent variable and independent variables is somewhat obvious based on the generated coefficients, the coefficients created from logistic regressions are more confusing because they're really referring to the log of the odds of the event happening. The methods of a logistic regression are similar to a linear one, in that it models the relationship between several variables, it just does so in a less straightforward fashion.

While that's sinking in, I'm going to backtrack a little. Before getting into the messiness of regressions, I wanted to see if there were any easy correlations to spot. The conditional probability charts below give a good idea of the magnitudes for possible ranges for FB%.

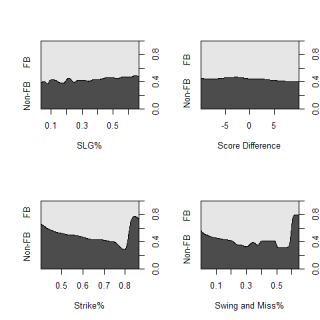
These charts graph the chance that a pitcher will throw a fastball on any pitch, based on one continuous variable. As slugging percent increases, the likelihood of seeing a fastball obviously decreases and there is an very (very) slight increase in the probability of throwing a fastball at the extreme ends of score differential. The two graphs on the bottom use two indicators of the quality of a pitcher's fastball. The graph on the left uses the percentage of a time the fastball is thrown for a strike while the one on the right uses the number of swings-and-misses generated as a percent of total swings taken at the fastball. Unfortunately, both graphs have several small sample outliers on the right that skew the graphs, but overall the trends are pretty strong and obvious. Good fastballs, both in terms of location and "nastiness" will be thrown frequently and these plots give an indication about what factors may be related to the likelihood of throwing a fastball.

Getting back to the regression, the first variable I tested was the 2006 slugging percent of the batter. Clearly there is a relationship between the amount of fastballs a hitter sees and his quality (I've beaten this point into the ground), but how strong is it? The coefficient for SLG was -.77, so for every .010 increase in SLG, the likelihood of seeing a fastball increases by .19 percent. This doesn't seem like that big of an impact, but is still a significant predictor of FB%. According to my regression, the factors that relate to the quality of a pitcher's fastball, the strike% and swing and miss% are also both significant factors if a pitcher threw a fastball.

Categorical variables, such as the count or the situation with base-runners are also important. This is again, a very obvious point, but as opposed to just looking at hitter's counts vs pitcher's counts, and saying certain types of batters see more fastballs in each type of count, with the regression, I can estimate what percentage of fastballs any type of hitter will see in any specific count. The chart below, which is a little confusing, attempts to do exactly that and also account for the quality of the fastball being thrown.

The green lines represent the estimated FB% in each count over a range of hitter abilities, for a fastball that gets a below average number of swings-and-misses. Looking just at the green lines, there are three relatively distinct bands. The top three lines (roughly starting around .8) are 3&0, 3&1 and 2&0, which are the three biggest hitter's counts. There are actually four separate counts in the next two distinct green lines (starting around .7), 3&2, 1&0, 0&0 and 2&1. The bottom cluster of lines has the remaining counts, 1&1, 0&1, 0&2, 2&2 and 1&2. These groupings end up matching pretty well with the groupings of counts found here.

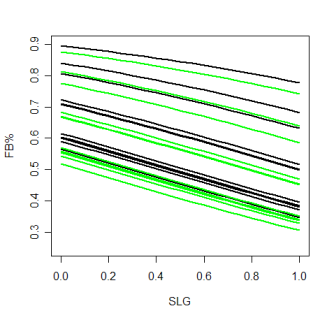
The black lines on the graph are estimates of the exact same thing (FB% in a given count over a range of SLG), but they are for pitches that have a higher than average swing-and-miss%. The ranges of different counts are the same so this just shows the range where most MLB pitchers would lie.

Before I wrap this up, I have a caveat to add. I only recently learned about logistic regression, so it's entirely possible that there is a problem with my methods. If anyone sees something I butchered with the regression, let me know and I'll fix it. I don't think this is the case or I wouldn't be publishing my results, but fair warning.

The differences I'm looking at right now are mostly marginal, especially at the ranges MLB players perform at. The three bands of counts are distinct in the FB% that pitcher's throw, but within each band, its very tough to see any differences. The next step with this type of analysis is to break down pitch selection based on potential swings in win expectancy. Win expectancy would account for score difference, base-runners, and outs, which are very important in determining how a pitcher pitches. The quality of the on-deck hitter is probably important as well.

On an individual pitcher level you could also potentially see more variation within a specific count. If Josh Beckett is throwing 70% fastballs in a 0&0 count while other Josh Beckett-types (pitchers with three pitches and a similar quality fastball) are throwing 60% fastballs in that count, that could be very valuable. Those numbers are for illustration, but a discrepancy like that would be important.