| Crunching the Numbers | February 11, 2010 |
I don't have any numbers crunched here, so I'm going to be relatively conservative and ask for someone--anyone--to tell me what the San Francisco Giants are doing strategically with their offers to Lincecum.
Let's talk game theory. The basic idea is that when there are two agents with potentially conflicting goals, the best strategy for each depends on their assessment of the best strategy of the other. The Lincecum arbitration case is an excellent example: there are two players, Lincecum and the Giants, in a zero sum game that determines Lincecum's 2010 salary (and beyond). The goal is pick a number that is closer to what an arbitrator would find to be a reasonable salary than your opponent does. Whoever picks the closer number is likely to win. If Lincecum asked for $43 million, the Giants could have offered $2 million and won. Clearly both sides are going to make more reasonable offers than that, but you get the point: the craziness of your offer depends on the perceived craziness of your opponents.
Lincecum's request, $13 million, is not too crazy. Its high, but he has no peers to be compared to. If you base his salary on his performance, and not his peers, $13 million is a bargain. If you look for the closest peer, its Ryan Howard who won his case for $10 million. The Giants offer was just strange: at $8 million, it was well below the previous highest-paid arbitration-set salary. I don't think many people would argue that Lincecum is worth 0.8 Ryan Howards. If Lincecum should be expected to make slightly more than Howard, say $11 million, a conservative figure, Lincecum's offer of $13 million is closer than the Giants $8. So the Giants appear to have low-balled Lincecum; not by a huge amount, but they low-balled him nonetheless. If we agree on a reasonable value of $11, the Giants would be expected to lose, but they could still have a decent chance of winning. In a non-trivial percent of possible universes, their team successfully argues their side and wins the day.
But I'd argue that game theoretic considerations make the Giants offer look really, really bad. First, the outcome of this arbitration hearing won't just affect Lincecum's 2010 salary; it will set the standard for his 2011 and 2012 salary as well. It will be easier for Lincecum to ask for $17 million in 2011 if he is making $13 million in 2010 as opposed to, say, $10 million. So the cost of losing this arbitration hearing is greater than the immediate costs of the $8 million bid. That means that another $2 million spent today saves a potential $4-6 million down the road. This would argue that both players should consider a conservative approach: make sure you win this hearing by bidding close to his true value. Its hard to argue that $8 million is close to his true value.
Second, what the Giants really want to do is sign Lincecum to a long-term deal. Lincecum will have an incentive to do so, given the likelihood for any pitcher to get injured. But by making such a low bid on the arbitration hearing, the Giants have put themselves in an awful negotiating position. Lincecum can expect to win his hearing and thus will be less likely to negotiate. If the Giants had bid, say, $10, there would be a very good chance they would win, which would put more pressure on Lincecum to accept a long-term deal at a price the Giants would prefer. If we were using game theory to build a model of this arbitration process, the potential for injury would be a force that drives down Lincecum's asking price. On the other side, however, it would not substantially affect the Giants estimate of his value. They could be expected to take out injury insurance to protect themselves from the possibility of Lincecum's arm falling off. The net effect is biased in favor of a long-term contract. I think the recent history of long-term deals being struck before arbitration hearings supports this principle.
So if the end goal was to tie Lincecum down for the long term at a good rate, why did the Giants choose to low-ball him? Their most recent offer to Lincecum is being reported to be at $37 for three years: $9.5, $12.5 and $15 respectively. Lincecum is reported to want a deal that starts at $13, not $9.5. Well, of course he does; if he doesn't make a deal, he'll probably make $13 next year. Why start at $9.5? The Giants offer would have had considerably more weight behind it if they had offered $9.5 up front.
In an alternate universe, the Giants offered $10.5 million in arbitration. They then offered $10.5, $13, $15.5 for the next three years. They would have had a very good chance of winning that hearing, and Lincecum would have had very good reason to take the long term deal. In this universe, it would be reasonable to expect him to get tied down for 3 years at under $40 million.
My general point is this: sometimes it is a better strategy to offer to pay more for a good or service. Sometimes a high initial bid will result in a lower long-term cost. The Lincecum arbitration may be just such a case, but the Giants swung and missed completely.
| Crunching the Numbers | January 13, 2010 |
Alternative title to this post: Why Tango Tiger still has a day job
I really enjoyed the feedback to my last article on why umpires should be biased in favor of control pitchers. Most of the folks with a solid statistical background responded favorably, while the unwashed masses thought I was ridiculous and should be run out of the blogosphere on a rail. (Perhaps I don't give the detractors enough credit; if they were washed and educated, then it was an equally entertaining Ask Marilyn-esque experience.) Anyhow, I thought I'd repeat the experience by picking on another low hanging fruit: betting on baseball games. I know a fair number of people who bet on sports. They don't understand that betting on sports is an investment in entertainment, not a viable means of turning baseball knowledge into cold hard cash. This post should be far less iconoclastic than the biased umpire post, but the central point doesn't appear to be widely known.
So here's the skinny: you should not bet on baseball. In the long run, you'll lose. No model that you can develop can be anticipated/demonstrated to beat Vegas. I don't care how good you (think you) are. I don't care how much you think any given line is outrageous. You can't be expected to win. You might think (as I did) that many people who bet on baseball may make poor predictions, and that the intelligent bettor may be able to profit off of them. You'd just have to be better than the average bettor, right? Wrong. I'd argue that Vegas profits off of these folks (because they set the lines), but the rest of us shouldn't get involved.
A couple caveats: First, I've been recording the Vegas odds for a couple years, and have analyzed data for 2007 and 2008. I forgot to download them this year before they disappeared off of the web service I use, so I don't have this year's odds. But I'd be happy to wager that nothing has changed because the system Vegas uses hasn't changed. Second, I am only looking at betting on who wins individual games; there are a number of other bets one could place, and maybe you could make money betting on which pitcher is most likely to start the top of the 7th inning, or which batter is likely to adjust their cup first. I'm not touching those wagers.
In 2008, Vegas came really close to being perfect. The variance between the actual outcome of all regular season games and Vegas' prediction for those games was within the range that one can attribute to random chance. If we start by assuming that Vegas' lines perfectly reflected the likelihood of each team winning each game, the variance between the predictions and the actual outcomes would be greater than it was in 2008 75 percent of the time.
That doesn't mean that Vegas is 75% likely to be perfect. We'd have to go all Bayesian and start assuming silly things to figure out precisely how good Vegas really is. But think about that statistic: if Vegas were perfect, they still would have had a 75% chance of making a worse set of predictions than they did in 2008. So somehow, by hook or by crook, they made some ridiculously accurate predictions in 2008.
It is still possible that the bookmakers got lucky, and that there is money to be made in betting on baseball. So I ran a couple more simulations. According to my numbers, it is crazy unlikely (p<.01) that Vegas is off more than 4% per game. This is because almost all baseball games have a true home-win probability of somewhere close to 50%. Even when the Yankees meet the Royals, the odds aren't far from 50%.
So let's run with my rough estimate that Vegas is off by no more than 4%. In order to make money betting on baseball, you'd have to do better than that. You won't make money if you're just better at chance (i.e., by picking the Yankees every time, or picking the home team every time). If you matched their 4% inaccuracy, you'd lose money a little more often than you won money (on a year-by-year basis). If you barely beat the 4% inaccuracy, with, say, 3.8% inaccuracy, you'd be expected to make a little money each year, but the likelihood that you would lose money each year would still be very high. If you removed 25% of the error in Vegas' estimates, so that your estimates deviated from the true probabilities by 3%, you'd make a profit 73% of the time (again, on a year-by-year basis...so 2-3 years out of every ten, you'd net a loss), for an average return of 3 cents on the dollar. I make more than that in my checking account (granted, it's a great rate for a checking account, but still...).
There are enough variables out there that there's a distinct possibility that I'm wrong. If you have the data to demonstrate that you can win reliably, I'd like to see it. But until then, I'm sticking with the numbers, which say that Vegas is really, really good, and you'd have to be considerably better (25% better) to even make a decent return on your investment.
I also have a novel answer to the question: "If you're so smart, why aren't you rich?" Because I'm smart enough to know it's a scam. Flame away :)
Update 1/14/2010
Following this post, there were a number of replies, mostly harsh ones. I expected nothing less, since there are far more people invested in baseball betting being a sound investment than the alternative. In fact, I was hoping for it; my initial analyses were run to see how large the margin for potential profit was for my own practical purposes. In the comments, I promised that if someone posted verifiable data that demonstrated that I was wrong, I would say so. I'm going to relax that standard and give Umaga credit for making a reasonable argument that I found convincing along with his own purported ROI.
Based on responses like those made by Umaga, I'll change my position: (1) No one can make money betting on the closing line, or lines that end up looking very similar to the closing line; (2) if you can predict which opening lines are particularly poor, and you bet early enough, you may be able to make money. In summary, I'd say that there are a small few (yes, likely financial quants, or ex-quants) who can leverage the peculiarities in the system to make money. I have no data for this, but I'm convinced that it's true. But for a vast majority of people, betting on something that looks like the closing line, you're not likely to make money.
Some have commented that a bookmaker's job is to balance the books, and to some extent to exploit known biases in bettors (such as to exaggerate the probability of a favorite, like the Yankees, to win). The story is that this pushes the moneyline away from the "true" probability of each team winning, creating a margin for people to put "smart money" in. I'm fully aware of how these lines are set, and how they change, but it doesn't change the story. If there are any biases such as these, the "smart money" is completely canceling them out. We know this because the closing line is as close to being a perfect measure of game outcome as is practically possible. It does not show the systematic bias that we would expect to see. Thus, if a bettor is going to exploit this, he would have to do so early, before the line drifts towards the closing line.
Others commented that I was being dense, and that "of course" the moneyline makes a "ridiculously good prediction" of game outcome. They argue that baseball betting is essentially a prediction market for baseball game outcomes. These comments absolutely miss the point: (1) a prediction market is not guaranteed to converge at a perfect prediction; (2) even if it *did* converge to the perfect prediction, the 2008 closing lines were better than you would expect a perfect prediction system to be 75% of the time. Kyle is wrong when he says "of course" bookmakers are that good; by random chance we would expect them to be measurably worse even if we predictive markets to converge to a perfect prediction (which seems to be Kyles other point, which, of course, is some combination of silly and naive).
The reason is this (in answer to TomC's question): every baseball game is a Bernoulli trial, that is there are two possible outcomes, home team wins and away team wins. There is a probability, p, that the home team wins, and a probability, q=1-p, that it loses. Thus, each baseball game is essentially a weighted coin flip. A perfect prediction system would have access to the "true" probability of each team winning (p and q). If you were to bet on whichever team has the greatest chance of winning, the outcome of your bet would also be a Bernoulli trial. This means that the variance between your optimal guess and the actual outcome has a known distribution: a binomial distribution. If we know the number of games we bet on, and we know the true odds of winning each of those bets, we can calculate a probability distribution for the variance between the actual outcome and our optimal guess. Thus, we can say things like "There is a 75% chance that the variance between our optimal guess and the actual outcome is less than some number, k."
In 2008, the variance between the bookmakers' closing line and the actual outcome was very small. In fact, it was less than we would have expected by chance 75% of the time.
What does that imply? If you were betting on the closing line, and you had perfect access to the true probability of each team winning, you would still have a 75% of being outperformed by (the average) bookmakers in 2008. If you can't outperform the bookmakers, you can't make money. Thus, you can't play the closing line, or lines that end up being similar to the closing line, and win.
But Umaga's point is a good one and well taken: I said both that you can't make money betting on baseball, and that you can't make money betting on the closing line. But these two claims are not equivalent. In the end, I'm convinced he is correct: I'll stand by the latter claim and back off of the former. You can't make money on the closing line, but you may be able to make money on the opening line or rogue lines (of which there are many). According to this story, making money on sports betting requires the bettor to be clever and look for opportunities to exploit, because the predictive market is really good. So for the vast majority of the sports bettors out there--the ones who don't have MBAs; who haven't had quant jobs at hedge funds; and who don't try to jump on opening lines before they drift away--those folks are buying entertainment every time they bet on a game.
Lastly, I'll point out that since bookmakers take a percentage of the action, this isn't even a zero-sum game; it's a negative sum game. One commenter, Garrett Weinzierl, doesn't like the implication that sports bettors are "all sailing off the edge." But since this is a negative-sum game, most bettors are sailing off the edge. For this system to work, most have to be sailing off of the edge. If you're a sports bettor, I'm not saying you're sailing in the wrong direction. Only Garrett knows where his boat is going. But if you're not at risk for going over an edge, you're an exception to the rule.
| Crunching the Numbers | December 20, 2009 |
In 2008, Jacoby Ellsbury was rated by Baseball America as the best defensive outfielder in Boston's minor league system. He made good on that prediction in 2008, impressing UZR and posting a 16.8 fielding RAA, 6.9 of which in centerfield.
In 2009, in the season Ellsbury was voted the Defensive Player of the Year by MLB.com, he was ranked by FanGraphs as having the worst defensive year of any center fielder, -18.6 runs. So which is it? Is he the best in the league or the worst in the league? Perhaps the MLB.com award was simply a popularity contest biased by a few web gems; there are a whole lot of Sox fans out there. That's possible, but I'm not quite willing to label Ellsbury the Derek Jeter of center field so quickly. Perhaps UZR isn't properly taking into account the peculiarities of Fenway? This isn't likely, given his rating in 2008 and that of Covelius in 2007.
It's been argued that Ellsbury is Jeter reborn: a poor defensive player who makes up for his deficiencies with flashy plays. The argument is that he makes poor reads off the bat and a poor initial step but makes up for it with his speed and a late diving catch. It's certainly possible, but looking over the video evidence, that's not my read. Some seem ready to dismiss Ellsbury on the basis of his UZR stat alone, but most fans don't seem to be so easily swayed. The fan scouting report over at The Book in 2008 and 2009 lists him as having an above average first step and average instincts (unlike Coco, who amusingly has incredible instincts, but the arm strength of a Girl Scout after a massive stroke).
On the other side, it's been argued that Ellsbury illustrates how meaningless defensive statistics are. No one has ever argued that defensive statistics are as definitive and meaningful as batting or pitching statistics, but to ignore them completely seems unwise. Theo Epstein seems to agree, given his moves to ship Mike Lowell--and his awful 2009 UZR--off to the Rangers while Boston pays his salary. I think the most honest observers have to admit that they just don't know how to reconcile the statistics with the widespread perception that Ellsbury is a good defensive player.
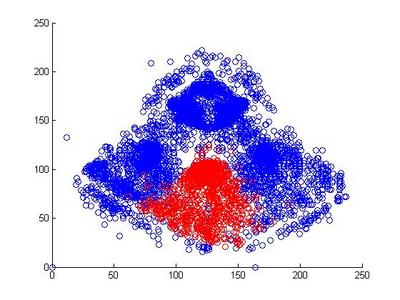
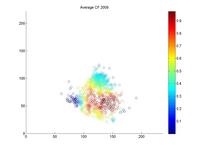
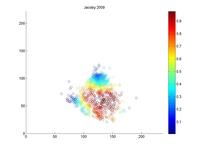
I looked at the pitch f/x data from 2008 and 2009 to get a sense of why Jacoby was being treated so poorly by UZR. Above is a plot of the 6500 plays at Fenway Park in which the x and y coordinates of the hit location was recorded. In red, I've highlighted all plays that involved the center fielder (each of these plays included the CF actually fielding the ball, either before or after it hit the turf. If the CF dove and missed, that isn't recorded by gameday). In each of the two years, we can look at the distribution of hits and outs that were fielded by all centerfielders playing in Fenway.
It's pretty hard to look to interpret these raw data, so I used a kernel density estimator to estimate the likelihood of each hit being turned into an out by either Ellsbury or the average CF playing in Fenway.
The blue circles in the scatter plots show hit locations from 2008 and 2009 that Ellsbury would have been less likely to have turned into outs; red circles show the locations Ellsbury would be more likely to turn into outs. Many of the circles are nearly white because there is no difference between Ellsbury and the average CF.
Gameday recorded a small minority of the actual hit locations, so it would be difficult to say anything conclusively even if there were strong patterns in the data (it's also unclear to me how many at-bats had zones recorded in the data that is used to calculate UZR. Retrosheet is missing hit locations for a vast majority of 2009 in Fenway). But it looks like Ellsbury didn't differ significantly from the average CF in 2008. In 2009, it looks like he may have been weaker at coming in on balls dropping in front of him, but there's no way to tell if that's pure noise. But what we absolutely don't see is the gaping hole you would expect to see in the range of the games worst centerfielder. Ellsbury seems to miss the plays that any CF would have missed, and seems to make the plays that any CF would have made. If I were a betting man, I would guess that Ellsbury's UZR will be league average next year.
| Crunching the Numbers | December 10, 2009 |
Jamie Hoffman isn't a great player by any means, and he is no longer a prospect, but the Dodgers have left him out to dry multiple times this year. If he was valuable enough for the Yankees to rise to the top of the Rule 5 Draft, why wasn't he protected?
Hoffman was the 18th best prospect in the Dodgers organization going into the year according to Scout.com, and 22nd according to Baseball America. He owns a AAA batting line of .285/.362/.449. He'll go into the 2010 season at age 25, and can play CF or RF. If he defense isn't quite good enough for CF, he projects to be a 4th outfielder, like a Gabe Kapler minus some muscle.
Hoffman was first designated for assignment on September 1st, passed through waivers, and then was resigned by the Dodgers. They did not protect him from the Rule 5 draft, however. The Dodgers made the choice to protect Trayvon Robinson instead of Hoffman, by adding him to the 40 man roster in November.
So why wasn't he on the 40-man roster, and why was he DFAed in September? The answer seems to be that he was redundant on the Dodgers. The 4th outfielder role is currently held down by Xavier Paul. Jason Repko also sits higher on the blue totem pole. I would have been surprised to see anyone grab Trayvon Robinson in the Rule 5 draft, but if the Dodgers perceived that as a threat, it could certainly be argued that he deserves protection more than Hoffman.
Perhaps it just says more about the Yankees than the Dodgers. The Yankees currently have 4 outfielders on the 40-man roster. The first two, Curtis Granderson and Nick Swisher, are clearly going to be penciled into most Yankees line-ups in 2010. The other two outfielders would be lucky to be penciled in at all. Melky Cabrera is a glorified backup centerfielder. He simply does not have the production to justify being played in a corner outfield position. With the Granderson acquisition, Melky will be reduced to being a 2nd choice centerfielder, and a last choice corner outfielder. The last outfielder, Brett Gardner is not even a good option for a 4th outfielder. How Gardner still has a job confuses me.
Hoffman would fit in well as a 4th outfielder. He can play any outfield position, and his production will likely justify his being played on a corner. He isn't a great base stealer, but he has speed on the bases, making him a good option as a pinch runner.
So this replacement-level outfielder, the 6th choice outfielder on the Dodgers, would be the starting left fielder on the current Yankees roster. This was clearly a good choice for the Yankees. It was also very bad planning on the part of the Dodgers if they had any interest in keeping Hoffman.
| Crunching the Numbers | December 07, 2009 |
I just wanted to post a short follow-up to a post from a few days back, Controlling the Zone in order to make what might appear to be a completely unreasonable assertion. Those are, after all, the best kind.
Umpires absolutely should be biased to give pitchers with good control a wider strike-zone. If an umpire does not give a pitcher with good control a wider strike zone, then he is being unfair.
The basic principle is this: if a pitcher has better control, then before you even see the pitch you should guess it will be a strike. If you see a borderline pitch that could go either way, you will be correct more often if you err on the side of calling strikes. That may not be too convincing, so let's do better.
Let's simplify this and look only at the lateral location of the pitch. Figure 1 shows a hypothetical distribution of pitches for a given pitcher. We'll assume that the distribution is normal along this dimension (this assumption is false for real pitchers, but that doesn't matter for our purposes here). In blue, we see the majority of pitches (60%) that fall between -10 and 10 inches from the center of the plate. These pitches are "true" strikes; they actually crossed the plate. The area in red represents the 40% of the pitches that fall outside the zone. These are "true" balls.
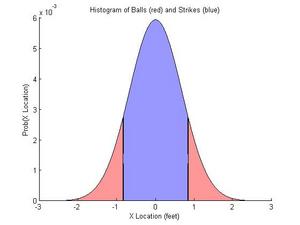
Figure 1. Histogram of "True" balls and strikes
Now let's assume that the umpire doesn't have direct access to the "true" location. Instead, he perceives the location of the pitch, but his perception has some uncertainty in it. Let's assume that the umpire will perceive the location of the pitch to equal the true location plus or minus a normally distributed error term. If we take the red distribution from figure 1 and convolve it with a Gaussian error term, we get the green distribution in figure 2. This green distribution represents where the umpire will perceive all of the "true" balls to cross the plane of the plate.
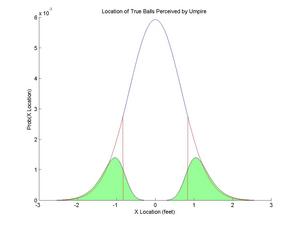
Figure 2. Histogram of the perceived location of "true" balls
Of these true balls, many appear to the umpire to cross the plate in the strike zone. That is, just the fact that the umpire is not perfect leads to some misclassifications. The green area in figure 3 reflects the true balls that are called strikes. In this figure, 16% of the actual balls are called strikes because of this error. But this isn't a bias; this error term will apply to all pitchers, regardless of their skill level.
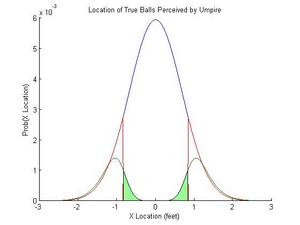
Figure 3. Pitches misclassified as strikes
The bias in the umpires perception comes in if he is trying to maximize his own performance, that is, make the fewest mistakes. The perceived distribution of pitches in figure 2 and 3 show how they would be classified if they were each considered in isolation. But we have a lot more information: we know the overall distribution of pitches. We know that a pitch closer to the center of the plate is more likely than a pitch outside. Therefore, our optimal guess, given the information and uncertainty that we have, is shown in figure 4. The green distribution in figure 4 shows the perceived location of the actual balls after the umpire takes his prior knowledge into account.
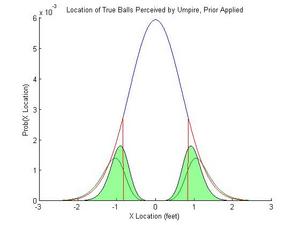
Figure 4. Pitches misclassified as strikes
Nearly 40% of the "true" pitches are now being classified as strikes (that's OK, some of the strikes are going to be misclassified as balls). Figure 5 shows the source of the misclassification. The area in red is the error caused by measurement error, the noise in the umpires perceptual system that causes him to be inherently uncertain. The area in green is caused by his priors, which will change depending on the context. If he faces a good pitcher with great control, the umpire's prior distribution should be very tight, with many strikes. If he faces Joel Zumaya, the umpire's prior distribution should be much more even (or even inverted, so that he is biased to call a ball).
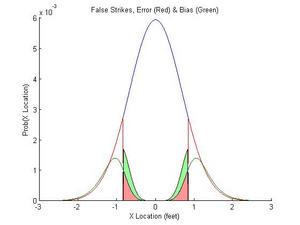
Figure 5. Pitches misclassified as strikes
Failing to take the context into account will result in impaired performance. The umpire would get more pitches wrong. If an umpire takes this "bias" into account, he is actually being as fair as he can be. If he did not use this bias, he would actually be unfairly biased against the pitchers with better control. What is fairness? Here, we would want the umpire to mistakenly call a true ball a strike as often as he calls a true strike a ball. If the umpire does not update and apply a prior based on the context, he is being unfair by this definition: when judging a good control pitcher, he will misclassify more true strikes as balls than vise versa.
Hence my initial claim: Umpires absolutely should be biased to give control pitchers a larger strike-zone.
This might be able to explain why the strikezone is a
All of that said, it's entirely unclear how an umpire should construct his prior, or what experiences should be used as a basis. Should it be based on a pitchers history? History with that umpire? The performance of that pitcher that day? The performance of all pitchers that day (not too unreasonable if the process is automatic)? The hypothesis becomes hard to test because the prior could be constructed in a number of very different ways.
| Crunching the Numbers | October 22, 2009 |
There has been a lot of good discussion of pitch classification in the past, but recently few algorithms have broken into the saber-blogosphere. So I'd like to take the opportunity to propose a classification framework for identifying pitch types that is probably novel to most of the pitch F/X community. It isn't perfect, but I feel that it makes a good step forward, and hopefully it will turn the community on to some new methods.
Machine Learning & Classification
Pitch identification is a classification problem. There has been a ton of academic work in physics, applied math and computer science on classification algorithms. There are your regressions (vanilla, logistic, multivariate logistic, sparse logistic, least angle, ridge , kernel ridge, etc), k-nearest neighbor, k-means, support vector machines, neural networks, principle components, independent components, latent Dirichlet allocation, hierarchical Dirichlet processes, Bayes nets, etc (see MVPA or PyMVPA for good toolboxes designed to make large multivariate pattern classification analyses easier). Many of these methods haven't made it out of the fields they were first introduced to (e.g., genomics, topic modeling), but they have some interesting applications to MLB pitch identification. I'll describe a type of probabilistic model, a Bayes Net, and show how it can be applied here.
Hierarchical Probabilistic Models
A Bayes Net is a generative graphical model which makes explicit a hypothesis about how the data were generated. For instance, pitch F/X data may have been generated hierarchically like this:
1. A pitcher, p, is chosen
2. A pitch type, tp is chosen for that pitcher
3. Pitch properties, Xtp = {velocity, movement, location} are randomly sampled from a multivariate normal distribution for that pitch, pitcher.
This might not seem like much, but it's a very useful formalism because it specifies the variables we think are relevant and the relationships between them. Here, the relevant dimensions are: pitcher, pitch type, pitch properties. The pitch properties depend on pitch type, and pitch type depends on pitcher.
Of these three variables, gameday gives us the pitch properties (movement, velocity and location), and the pitcher identity. The pitch type variable is a latent (unobserved) variable that we hypothesize mediates the relationship between the pitcher and the pitch parameters. The goal is to use the variables we have observed and the hypothesized relationships to evaluate the latent variable, pitch type.
In the end, the probabilistic model works much like a regression. A regression tries to find the single best linear model (the maximum likelihood estimate for the model parameters). Similarly, the probabilistic model work tries to maximize the likelihood of the observed data, given our model. It simultaneously tries to fit pitch-types to pitchers and pitches to pitch-types.
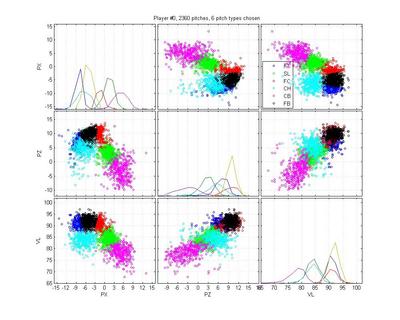
Centers of mass for each pitch type across pitchers, normalized by fastball speed
To illustrate how this works, consider a simple example: two pitchers throw an 85 mph pitch that could be a fastball. For pitcher A, it actually is a fastball and for B it is a change-up. For each pitcher, the model will consider the cluster of pitches that looks most like a fastball (for that pitcher). For the pitcher A, there will be nothing faster than the 85 mph pitch. This will cause the algorithm to shift the FB category down, so that it treats 85 mph pitches as fastballs. It will then push the CH category even further down in search of another cluster. For pitcher B, the 85 mph pitches don't look as fastball-y as his 95 mph pitches, which have to be fastballs. This causes the algorithm to shift the FB category up to 95 mph. The CH category will then sweep in to 85 mph fill the gap. Only by using information about the pitchers other pitches can we successfully discriminate between these two pitch types.
Park Effects
There has been some good work looking at differences in the pitch F/X set-up at different parks. I first corrected all of the pitch F/X data by removing the average park effects for each park-year.
Heuristics
I built in some heuristics to reflect our knowledge of the game. Analysts are very good at pitch classification, so why not just copy them? A brainstorming session over at The Book Blog proposed the idea of classifying the fastest pitch as a FB, and the slowest as a CB, and then classifying other pitches relative to these bounds. That works well with this algorithm because estimating the parameters is an iterative process. So we can first guess which pitches are fastballs, and then use the speed of those fastballs to help us figure out the identity of other pitches. As we iterate, our guesses for which pitches are fastballs will change gradually, as will our estimated fastball speed. If the algorithm works, it will converge on the "true" fastball speed, and allow us to use this information to inform our decision about other pitches.
Results
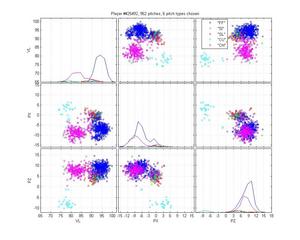
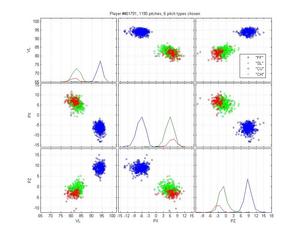
The goal was to achieve 98% accuracy. We're not there yet, but I'll you decide how far away we are. I've randomly selected some pitchers (I skipped the boring cases where classification was easy) to illustrate it's success. I think this selection represents the strengths and the remaining weaknesses of the model.
Russ Ortiz
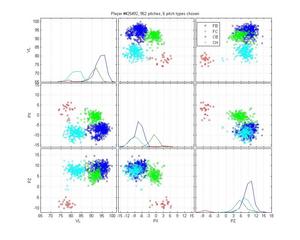
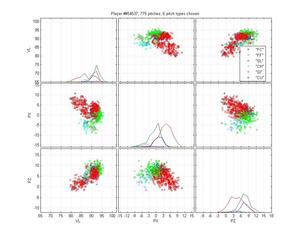
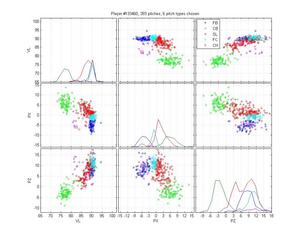
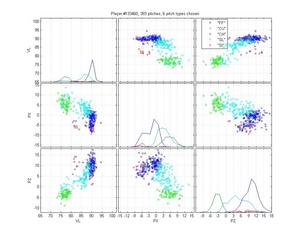
I like Ortiz because he provides a particularly nasty problem for pitch classification (even though the HPM does not perfectly categorize his pitches). His curveball is obvious, as are his change-ups. But he has two very similar fastballs and his slider is right in there too. The MLB classification is pretty poor: they give him one fastball that spreads from 0 to -9 inches of lateral movement; they mix sliders up with both fastballs and curveballs; and some of the change-ups are classified as sinkers. The HPM classifies his fastball into two groups, which looks right to me. It falls prey to one of the problems of the MLB classification, though, by letting the SL cluster nibble on the edge of the FB cluster. That's clearly wrong.
HPM classification (left), MLB classification (right)
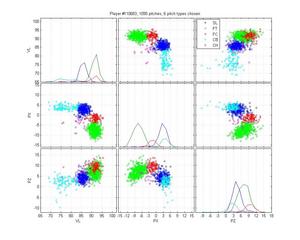
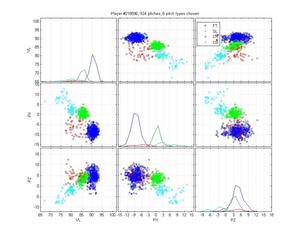
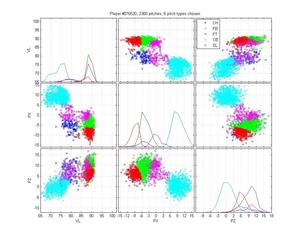
Ryan Madsen
Neither pitch classification system notices that Madsen throws a 2-seamer, but its hard to blame them; it overlaps pretty well with his fastball. The HPM is really solid otherwise, whereas MLB is really confused about his cutter.
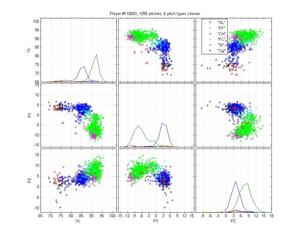
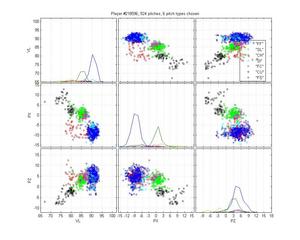
Miguel Batista
Batista poses another interesting problem because he throws a cutter and a sinker and, who knows, there may be a 4-seamer in there too. The MLB classification is pretty poor: it only calls a small portion of his sinkers as sinkers, and none of the cutters as cutters. Instead, it calls some sliders as cutters. It also really confuses curveballs and change-ups. Again, the HPM is not perfect: The curves are nibbling in on the slider cluster, which is clearly wrong. It also may be calling too many pitches change-ups. Hard to say. But the difference is still night-and-day.
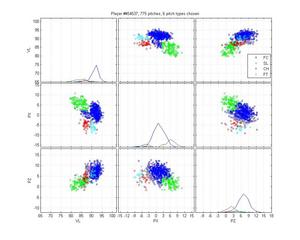
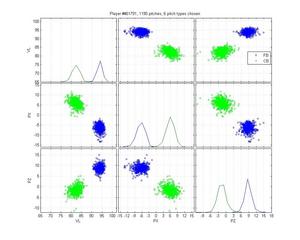
Jared Burton
Burton is an example of a relatively easy case that MLB screws up horribly. Its remarkably inaccurate. The HPM model isn't up to snuff either, but it does better. I honestly can't say how I would classify the cluster below the cutter; is it an extension of his slider cluster? That would be my guess, but with low confidence.
Tim Hudson
The HPM may be overly enthusiastic about the change-ups, and I think the classification of sliders and curveballs is potentially arguable, but overall I'm happy with it. The MLB classification, on the other hand...
Carlos Marmol
Marmol is a really, really easy classification, but MLB still gets it wrong by splitting his slurvy pitch half and half into sliders and curveballs. I don't really care about the labels--we could call it a luxury yacht for all I care--as long as all the pitches of the same type are given the same labels.
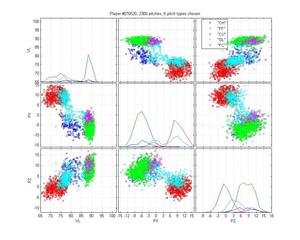
Bronson Arroyo
Arroyo is an absolute nightmare for pitch classification algorithms. I have difficulty figuring out what he actually throws. He has two fastballs, but they have a huge variance and are highly overlapping. What is going on with that change-up? Is it that inconsistent, or is there a ton of noise in these data? His slider and his curve are highly overlapping as well. I don't even want to venture a guess as to the type of the pitches that fall between his fastball and his slider. In this case, the HPM is absolutely clueless and in some ways worse than MLB. It really gets thrown by that train of pitches that straddle the FB-SL divide, which pulls the SL cluster up into the gap between FB, CH and SL. It also doesn't do a good job of separating the FB and FTs. But I always expected some failures, and this is at least an understandable one.
Some Remaining Problems
The biggest problem with this model is that the underlying generative model is wrong. We have to assume that all pitchers throw the same number of pitches. That leads to some problems for some pitchers. The "nibbling" of the corners of a cluster by another pitch-type is caused by extra pitch types that the pitcher doesn't throw sitting between groups.
That leads to a second problem with the model: it tries to maximize the likelihood of the observed data, but it doesn't care if it predicted a lot of pitches in a region where there are none. Essentially we are giving it credit for hits without penalizing for false alarms. This is what causes extra pitch-types to float into the spaces between groups, like in Bronson Arroyo's case.
Third, there is Bronson Arroyo. I think the solution is for him to retire.
| Crunching the Numbers | October 05, 2009 |
A couple days ago, Dave Allen deconstructed Mariano Rivera. He commented that he had never seen any other pitcher who could locate his pitches with the same kind of bimodal distribution of pitches along the lateral dimension. I noticed the same thing when I ranked Rivera as having one of the best fastballs in baseball. But I was curious: how unusual is Mariano's X location distribution? Is he among the best in hitting the corners?
No. He is the best.
A quick SQL query produced the lateral distance from the edge of the strike zone (10 inches from 0 in the pitch F/X data) for all pitches measured by GameDay since 2007. Amongst all pitchers with 100+ pitches recorded, Mariano Rivera has the lowest average distance from an edge. On average, he places his pitches 4.4 inches away from the very edge of the plate.
Here are the top 10:
- Mariano Rivera, 4.43
- Tom Shearn, 4.57
- Jorge Campillo, 4.67
- Woody Williams, 4.69
- Chad Cordero, 4.72
- Scott Elarton, 4.74
- Scott Atchison, 4.75
- Keith Foulke, 4.76
- Chris Lambert, 4.77
- Leo Rosales, 4.80
Many of these guys have 85 mph fastballs. It's tempting to think that the only reason they can survive in the majors is because they paint the corners. Rivera is really the only one of the bunch that has fantastic stuff to go along with such pinpoint control. Hence his dominance.
Here is a graph of Mariano Rivera's locations with #3 Jorge Campillo's locations for comparison (click on the graph to enlarge).
Update: Shawn pointed out that this isn't an impressive group of pitchers. I think one could argue that most of the guys with exceptional command lack the velocity to survive in the majors without that command. But lets remove the chumps by only looking at pitchers that have thrown more than 200 pitches that exceed 90 mph. Here's the new list:
#1 Mariano Rivera, 4.41
#3 Kyle Lohse, 4.65
#4 Grant Balfour, 4.75
#5 Jared Weaver, 4.77
#6 Kyle Kendrick, 4.78
#9 Clay Buchholz, 4.84
#10 Ross Ohlendorf, 4.85
#12 Joakim Soria, 4.87
#13 Brandon Lyon, 4.89
#19 Zack Greinke, 4.89
If you only look at pitches that are in the zone (within a foot of the center of the plate), Mariano takes an even bigger lead, but is joined by Jon Garland, Carlos Silva, Roy Halladay, Francisco Cordero, John Smoltz, Matt Garza and Jeremy Bonderman in the top 25.