
| Designated Hitter | April 16, 2009 |
Perhaps the widest and deepest pitfall lying in wait for any who deal in numerical analyses is forgetting the distinction between precision and accuracy. If I state that Team X's opening-day first pitch was delivered at 1:07:32 pm, I am being quite precise; but if in fact it was a night game, then the statement that the pitch was made sometime between 7:35 and 7:40 pm, though far less precise, is far more accurate.
It is all too easy to be hypnotized by the ability to calculate some metric to a large number of decimal places into believing that such precision equates to accuracy. As a case in point, let us look over the concept of "park factors". It is undoubtable that ballparks influence the results that players achieve playing in them, and in many cases--"many" both as to particular parks and as to particular statistics--those influences are substantial. Park factors are intended as correctives, numbers that ideally allow inflating or deflating actual player or team results in a way that neutralizes park effects and give us a more nearly unbiased look at those players' and teams' abilities and achievements. So much virtually everyone knows.
The idea behind the construction of park factors, stated broadly, is to compare performance in a given park with performance elsewhere. As an example, a widely used method for educing park factors for a simple but basic metric, run scoring, is the one used by (but not original to) ESPN. The elements that go into it are team runs scored (R) and opponents' runs scored (OR) at home and away, and total games played at home and away.
(Rh + ORh) ÷ Gh
factor = ───────────────
(Ra + ORa) ÷ Ga
That comes down to average combined (team plus opponents) runs scored per game at home divided by the corresponding figure for away games. Let us see what some of the things wrong with that basic approach are, and if we can improve on it.
A "park factor" is supposed to tell us how the park affects some datum--here, run scoring. Perhaps the most obvious failing of the ESPN method is made manifest by the simple question compared to what? In the calculation above, run scoring at Park X is being compared to run scoring at all parks except X. Thus, each park for which we calculate such a factor is being compared to some different basis: the pool of "away" parks for Park X is obviously different from the pool of "away" parks for Park Y (in that X's pool includes Y but excludes X itself, while Y's includes X but excludes Y itself). Now that rather basic folly can be fairly easily corrected for; let's call the average combined runs per game at home and away RPGh and RPGa, respectively. Then, if there are T teams in the league,
RPGh
factor = ───────────────────────────────
{[RPGa x (T - 1)] [RPGh]} ÷ T
But there remain considerable problems, the most obvious being that the pools are still not identical, in that schedules are not perfectly balanced: Teams X and Y can, and probably do, play significantly different numbers of games in each of the other parks. Even if we throw out inter-league data, which is especially corrupt owing to the variable use of the DH Rule, we still have differing pools for differing teams, at least by division (and possibly even within divisions, owing to rainouts never made up). Well, one thinks, we can see how to deal with that: we would normalize away data park by park, then combine the results, so the "away" pool would, finally, represent the imaginary "league-average park" against which we would ideally like to compare any particular park's effects.
Let us remain aware, however, before we move on, that there are yet other difficulties. We have been using the simple--or rather, simplistic--idea of "games" as the basis for comparing parks' effects on run scoring. But even at that level, there are inequalities needing adjustment, in that the numbers of innings are not going to be equally apportioned among home batters, away batters, home pitchers, and away pitchers, in that a winning team at home does not bat in the bottom of the last inning. There is also the further question of whether innings are the proper basis for comparison. For most stats, the wanted basis for comparison is batter-pitcher confrontations, whether styled PA or BFP. But there are complexities there, too. A batter's ability to get walked, or a pitcher's tendency to give up walks, might seem best based on PAs or BFPs; but higher numbers of walks mean a higher on-base percentage, which means that more batters will get a chance to come to the plate (it is that "compound-interest effect" of OBA that is often not properly factored into metrics of run-generation, individual or team: not only is the chance of a batter becoming a run raised, but the chance of getting that chance is also raised). That will increase run scoring in a manner that a metric measured against PAs will not fully capture. And there are yet other questions, such as whether strikeouts should be normalized to plate appearances or to at-bats.
But for our purposes here--getting a grand overview of the plausibility of "park factors"--such niceties, while of interest, can be set aside. Let's look at the larger picture. Let's say we want to get a Runs park factor for Park X. We have seen that we need to use normalized runs per game on a park-by-park basis if we are to avoid gross distortions from schedule imbalances and related factors. How might that look for a real-world example? Let's take, arbitrarily, San Francisco in 2008. Here are the raw data:

And here are the consequent paired raw factors:

But, because we have used a particular park for these figurings, all those numbers are relative to that park. What we want are numbers relative to that imaginary "league-average" park. For example, if we had chosen the stingiest park in the league, all the factors would be greater than 1; had we chosen the most generous, all the factors would be under 1. But all we have to do is average the various factors--in which process we assign the park itself, here San Francisco (I refuse to use the corporate-name-of-the-day for that or any park), a value of 1, since it is necessarily identical to itself--and then normalize the factors relative to that average. When we do that, we get what ought to be the runs "park factor" for each National-League park relative to an imaginary all-NL average park:

The average is not exactly 1.000 owing to rounding errors, but it's close enough for government work. If we sort that assemblage, it looks like this:
But before we jump to any conclusions whatever about those results, let's ponder this: they were derived from data for one park, one team. Yet, if the methodology is sound, we ought to get at least roughly the same results no matter which park we initially use. Imagine a Twilight-Zone universe in which the 2008 season was played out in some timeless place where each team played ten thousand games with each other team, yet still at their natural and normal performance levels as they were in 2008. Surely it is clear that we then could indeed use any one park as a basis for deriving "park factors" since, in the end, we normalize away that park to reach an all-league basis. In that Twilight Zone world, any variations from using this or that particular park can only be relatively minor random statistical noise. San Francisco is to Los Angeles thus, and San Francisco is to San Diego so, hence Los Angeles is to San Diego thus-and-so (in a manner of speaking). So what do we see if we try real calculations with real one-season data? Let's continue with the National League in 2008. Shown are the "park runs factors" for each park as calculated from each of the other parks as a basis. If the concept is sound, the numbers in each row across ought to be roughly the same. Ha.
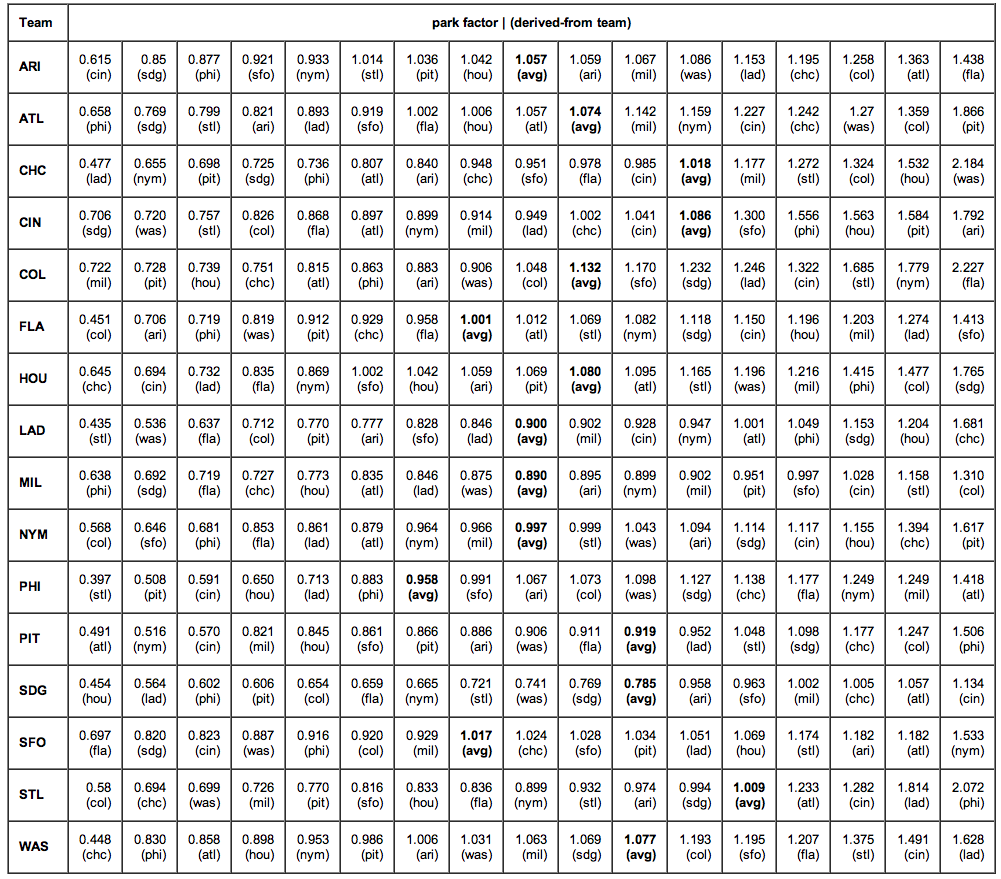
Well, now we know something, don't we? This just doesn't work. But it's not the methodology. Nor is it the various minor factors we saw earlier: those don't produce 3:1 and greater spreads in estimation. No, what we are dealing here, plain and simple, is the traditional statistical bugaboo--an inadequate sample size. Here is a possibly instructive presentation: the averaged run-factor values from that table above compared to what the simplistic ESPN formula yields:
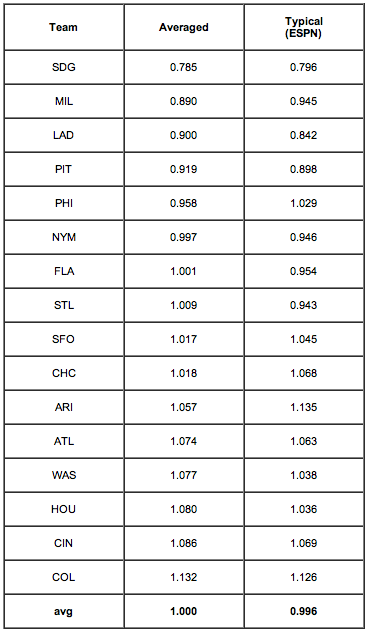
Instructive, indeed. The agreement is not perfect, as we would not expect it to be. The "average" column is a little better than the ESPN column because it allows better for the differing numbers of games on the schedule, but by using the average for each park of the values derived from all the other parks we are approximating the ESPN method.
The entire point of this lengthy demonstration has been to lift the lid off those nice, clean-looking, precise park-effect numbers to show the seething boil in the pot. The end results are not totally meaningless: we can say with fair credibility that San Diego's is a considerably more pitcher-friendly park than Colorado's, and that the Mets and the Marlins were playing in parks without gross distorting effects. But to try to numerically correct any team's results--much less any particular player's results--by means of "park factors" is very, very wrong.
But wait, there's more! (As they say on TV.) If the problem is a shortage of data, why not simply expand the sample size? Use multi-year data? That would be nice, and useful, were no park changed structurally over a period of some years. But consider: not even counting structural changes, in the last ten seasons (counting 2009), a full dozen totally new ballparks have come on line. When one considers that pace, plus the changes (some even to a few of those new parks), it becomes painfully obvious that trying multi-year data is as bad or worse. Even for a particular park that might itself not have been at all changed for many years, there remains the issue that the standard of comparison--that imaginary league-average park--will have changed, probably quite a lot, over that time, owing to changes in the other real parks. So we can't use multi-season values, and single-season values are comically insufficient for anything beyond broad-brush estimations, estimations more qualitative than quantitative.
I should point out that none of this is today's news. In 2007, Greg Rybarczyk at The Hardball Times noted that the home-run "factor" for the park in Arizona was 48 in one season and 116 in the next. Back in 2001, Rich Rifkin at Baseball Prospectus remarked that "Unfortunately, it is problematic to average out a park factor over more than a few years because the conditions of one or more of the ballparks in a league change. New stadiums are built, existing stadiums change their dimensions, and abnormal weather patterns have an impact." (Regrettably, the next sentence was "Nonetheless, a 10-year sample is likely to be more accurate than a one-year accounting.") Probably the defining essay on the subject is the 2007 paper titled "Improving Major League Baseball Park Factor Estimates", by Acharya, Ahmed, D'Amour, Lu, Morris, Oglevee, Peterson, and Swift, published in the Harvard Sports Analysis Collective. But, justifiably proud as they are of their improved methodology, even they concluded that "Unfortunately, the lack of longer-term data in Major League Baseball . . . makes it extraordinarily difficult to assess the true contribution of a ballpark to a team's offense or defensive strength."
Precisely accurate.
Eric Walker has been a professional baseball analyst for over a quarter-century. His paper "Winning Baseball", commissioned by the Oakland A's for the purpose, first instructed Billy Beane in the concepts later called "Moneyball"; Walker has also authored a book of essays, The Sinister First Baseman and Other Observations. Walker is now retired, but maintains the HBH Baseball-Analysis Web Site.
Comments
Regrettably, the next sentence was "Nonetheless, a 10-year sample is likely to be more accurate than a one-year accounting."
Isn't this true, though? Given that the error in single season park factors is so large, wouldn't a 10 year sample be more accurate than a 1 year sample?
Posted by: jeremy at April 16, 2009 8:34 PM
Jeremy,
10-year sample should reduce random error, that's what increase in sample-size is for. But if the increase in sample-size introduces systematic error, resulting error can be larger than 1-year sample. For example, when Royals pulled fences in, they made their park more hitter-friendly, and every other park in the league more pitcher-friendly. Any data set that has data from both old and new configuration will introduce systematic error in the calculation and for AL Central stadiums that error may be larger than random error of 1-year sample.
Posted by: DR at April 17, 2009 3:31 AM
Eric,
First off, great work. Park factors have bothered me for a long time, and you articulating what I did not have the patience nor the math skills to do.
My big question becomes where precision and diminishing returns meet. As you suggest, we know directionally from different park factor methods that Petco supresses runs and Coors increases them. The question becoems, in my mind, is how precise do we need to be for the information to be useful? And at what point are we chasing a statistical 'over-engineered' measure? Or better put, how precise do we need to be to get better analysis?
Posted by: Adam at April 17, 2009 1:33 PM
First, yes, the point is that the changes from year to year in parks--structural changes of consequence to performance or, often, entirely new parks--makes multi-year data even worse than one-year data. Remember again that it is not only the stability of Park X that matters, but also the stability of the pool we are comparing it to, that imaginary all-average ballpark; when that changes significantly, as it does virtually every year, it renders multi-year data worthless for comparisons.
Second, and related, my belief, which I think the rows and columns of the big table bear out, is that we simply cannot with any shred of honesty apply numerical park corrections to any statistic. To multiply, say, runs by 1.05 is dishonest if we know that the correct figure might be, say, anywhere from 0.85 to 1.25 (and the true range is probably worse).
I believe--I assure you, with much regret, that we just have to bite the bullet and be more qualitative than quantitative: yes, those are Colorado results, so take them with a handful of salt--that sort of thing. We all love hard numbers, but park factors are very soft, squishy numbers.
Posted by: Eric Walker at April 17, 2009 4:03 PM
Eric,
Thanks for the mention and the kind words. Subtle distinction - our paper was published in The Journal of Quantitative Analysis in Sports and presented at The New England Symposium on Statistics in Sports. The Harvard Sports Analysis Collective is the student group.
Posted by: Bobby Swift at April 18, 2009 9:46 AM
While the "primer" by Eric is instructive and caution should always be taken when adjusting team or player stats using PF's...
There are several problems with his thesis:
First of all, all of the issues he speaks of can be handled, statistically, with no problem whatsoever, if one has the know-how and takes the time to do so. So let us not throw the baby out with the bath water by declaring that "All PF's are next to worthless, don't work, cannot and should not be used to adjust player and team stats, etc."
More importantly, even a "bad" park factor can be useful and can be used appropriately.
In fact, consider this statement by Eric:
"The end results are not totally meaningless: we can say with fair credibility that San Diego's is a considerably more pitcher-friendly park than Colorado's, and that the Mets and the Marlins were playing in parks without gross distorting effects. But to try to numerically correct any team's results--much less any particular player's results--by means of "park factors" is very, very wrong."
He is 100% correct in the first part. That obviously there is SOMETHING even in "bad" park factors that is able to give us useful information. Even a "bad" PF generally tells us that COL is more of a hitter's park than SD or WAS and that TEX is more of a hitter's park than OAK. So there must be SOME good information in PF's, which there is of course. It is good information combined with noise (and perhaps some biases).
The last part of his statement is flat out wrong, considering the first part. If the first part is correct, which it is - that even a sloppy PF gives us some useful information, then it HAS to be correct that we can use those PF's to adjust player and team stats so that or adjusted stats more accurately reflect a player or team's performance in a park neutral environment. HAS TO!
That does not mean, however, that we have to use a "bad" park factor as the purveyor of that PF wants us to use it. For example, let's say that our "bad" PF tells us that Coors inflates runs (as compared to the whole league) by 20% and that Petco deflates it by 10%. Even Eric would agree that while he does not trust those numbers exactly, that they probably are on the right track and are somewhat in the ballpark, no pun intended.
But he, and other "PF naysayers" don't want us to use those PF's to adjust player and team stats, apparently, at least according to the last part of the statement from him I quoted above.
Poppycock!
Would it be better to, say, take a run scored in Coors (by some team, player, or whatever) and do nothing or would it be better to say, adjust it by 1% (even though our "bad" PF says to adjust it by 20%)? If you said, "Better to adjust (by 1%) then not adjust at all, you would be correct!"
What about Petco and adjusting by 1% versus not adjusting at all? Same answer. I hope everyone gets my point so far.
So, it is not that these "bad" PF's are not useful, it is that it is not necessarily correct to use the exact numerical adjustments that the purveyors of these PF's might want you to use - for example 20% for Coors and 10% for Petco.
So the answer is not to "not use them at all" which is (incorrectly) throwing the baby out with the bathwater. The answer is for YOU to figure out how much of the actual PF that some system comes up with to use. You do that by evaluating the rigor of the system and how much data it uses. For example, there is absolutely NO reason not to use, for example, at least half of a run factor derived from a system that takes into consideration each team's schedule and year to year changes in parks and uses 10 years worth of data. (And by the way, using 10 years of data in just about any PF "system" is going to yield a number that is more accurate than the same system using 1 year numbers almost no matter what, and it is not going to even be close, as long as that system is halfway decent).
Getting back to the Coors and Petco example above and the "bad" (but still reasonable, like the ESPN one) PF system that gives Coors a 120 rating and Petco a 90 rating, so if most of us are in agreement that it would still be correct to adjust Coors and Petco numbers by 1% (in opposite directions of course), then what about 2%? How about 5%?
Where do we cross the line from improving our numbers (by doing SOME adjustments) to doing worse than nothing at all? I don't know the answer to that as it depends on, as I said, how the particular system is constructed (is it a good one or not), but I can tell you that for almost any halfway decent system you can always use a little bit of a park factor to neutralize performance and do better than nothing at all. And even if 120 and 90 are not correct, it STILL might be better to use the entire numbers than do nothing at all!
Let's say that the real numbers are 115 and 95, which would not be unreasonable for a system that gets 120 and 90 (there is always going to be regression towards 100). Do you think using 90 and 120 to adjust player and team numbers would be better or worse than using nothing at all? Again, if you said better, you would be correct!
Posted by: MGL at April 20, 2009 1:43 AM
I just cannot grasp how arguments like this can be advanced. You cannot make a silk purse out of a sow's ear of inadequate data. If I have raw data, say runs per game, that are exactly equal for two different parks, and I then "adjust" those data by park factors (calculated I don't give a flying wahoo how), I might get, say +10% for one and -5% for the other--when, as the table data show, the reality could as well be more or less exactly the opposite. I don't know how loudly I can shout it, but WE CANNOT KNOW. You cannot extract conclusions from grossly inadequate sample sizes, and no magic can change that. To paraphrase Gertrude Stein, Inadequate data is inadequate data is inadequate data. For example, half of the attempts to get merely a runs factor for a park as extreme as Colorado is thought to be show it as less than 1. Even restricting ourselves to only the other teams in the same division still shows one value well under 1. All told, sure, Colorado is pretty surely a hitter's park, as common experience suggests, but to dream that we know well enough how much of one--even in this extreme case--to have the nerve to "adjust" data is farcical.
The claim that "'PF naysayers' don't want us to use those PF's to adjust player and team stats" is a half-truth: I, at least, would love to have park factors usable to adjust obviously biased data, and for years--back when new parks were unusual occurrences and structural changes in older ones not common--I calculated and used them. But I indeed do not myself today use "those PF's", nor would I put much trust in any who do, because such PFs are not numbers, they are doodles, about as like to make the errors worse than better while yet presenting those diddled results as if they are some sort of improvement on the historical raw originals. Till MLB issues a flat 10-year ban on all new parks and structural changes to extant ones (standard advice about repressed respiration), meaningful park factors will remain a pipe dream.
This is not religion, where you pick a doctrine to believe in because it appeals to you: it is numerical analysis, and if someone knows a method for getting meaningful measures from meaningless sample sizes, I'd be pleased to hear of it.
Posted by: Eric Walker at April 20, 2009 2:48 AM
MGL is correct that something is better than nothing. He is also correct that if you use too much, it might be worse than using nothing.
Take the case of Barry Bonds. He has had substantial playing time at SF's home park. The number of HR he hit at home and on the road in his SF years are virtually identical. But, if you look at all other LHH, you will find that SF depresses HR by 33%.
If you look at Juan Pierre at Coors, you will find that his HR rate does not change. If you look at Dante Bichette, you will see that it changes substantially.
The real danger is using a one-size-fits-all park impact number, when each player is unique. In the case of Bonds and Pierre, no park impact number is better than using any. In the case of Bichette, you come to the opposite conclusion.
The real position to take is that current park impact numbers gets you from step A to some intermediate step, when we still have to get to step Z. Some people believe that that intermediate step is step B or C, and others believe it's step X or Y.
Posted by: tangotiger at April 20, 2009 7:19 AM
I mean Barry's latest SF home park, which has been known as Pac Bell, SBC and now AT&T.
Posted by: tangotiger at April 20, 2009 7:23 AM
"For example, half of the attempts to get merely a runs factor for a park as extreme as Colorado is thought to be show it as less than 1."
If you break down a sample into small enough pieces, won't things always appear quirky? Why not take the team vs. team route to the extreme: compare one home game to one away game for each team-team pair? Holy noise!
What we really care about are the error bars on a PF. In the article, Eric claims they could be larger than +/- .20. I doubt they're that large, once you use multiple seasons worth of data and properly regress. Anyone else who's looked at PFs care to show what errors bars we can expect?
Posted by: Sky at April 20, 2009 8:08 AM
Eric is right that they could get pretty large if you are using it on individual players (which is REALLY what we ultimately care about).
No one is going to convince me that Pac Bell has had a depressing effect on Bonds' HR total anywhere close to the 33% drop other LHH have suffered there. Indeed, it would be fairly difficult to convince anyone that it's had anything more than a smidge of an effect on Bonds himself.
The uncertainty level of a park impact to each hitter will be fairly large. That's not to say that you should do an adjustment. But, if you decide to realign Bonds using all other LHH hitters, you will need to add 50% to his home HR totals (if you use a multiplier) or +.01 per home PA (if you use the additive method). Or somewhere in-between if you use the Odds Ratio Method.
Posted by: tangotiger at April 20, 2009 8:48 AM
Eric,
If your point is that the ESPN numbers are not perfectly accurate, I agree with you.
How accurate do you think they are? Saying that they're "comically insufficient" may be true, but that statement is not useful unless it's quantitative. In numerical terms, how useful or accurate are they? Are you saying that the 95% confidence intervals for parks are so wide that they all embrace 1.000? Are you saying they're even wider?
Can you be a little more quantitatively precise so that we can evaluate your claim?
Posted by: Phil Birnbaum at April 20, 2009 9:05 AM
(Sorry for the delay: I've been--and still am--running a mild fever, and not been up to doing much.)
I think at this point that rather than try to answer a potentially endless series of "but what about/but what if" queries, I'd like to see the thing turned around. If meaningful park factors can be derived, let's have someone present the methodology and actually do it, using real-world numbers. Take into account not only the several things already mentioned, but these, too: most or all parks are, at least anecdotally, held to play nontrivially differently at night versus in the day, so either demonstrate that that is not so or show how the distinction is normalized out; ditto for handedness of pitchers; ditto for stadia with retractable roofs. (Other matters may also occur to you.)
As a criterion for "meaningful", imagine that you are employed by a team that could sign either, but not both, of two players who each have an established history at some park, but not the same park, and who have essentially identical raw stats, and whose GM asks you, his house wizard, which is the better hitter. On your answer, which you propose to obtain by applying your park factors, may ride several million dollars of the team's money, the team's record over the next season or three, and certainly rides your prospects for continued employment by that team and possibly in the industry. Park factors that you would feel happy using in that case--that you are confident will not mistakenly identify which is the better man--are what are wanted.
Posted by: Eric Walker at April 22, 2009 11:21 PM