What happens when you combine Hit Tracker data with Pitch f/x data? You get a whole lot of data.

First, I looked at batter age in relation to standard home run distance. Standard home run distance is the distance a home run would travel in neutral conditions if it were to land at field level. My sample contains data on home runs from 2007 and 2008, totaling nearly 10,000 data points.

It appears to me that the age 25-29 peak holds true. I had data on 16 homers hit by players before their 21st birthday and the average distance was 420 feet. This is because Justin Upton is an absolute monster. The oldest grouping of players is likely biased since players who maintain the ability to hit home runs at that age are almost entirely power-happy first basemen and designated hitters. That group will be lighter on lighter-hitting middle infielders than the younger groups.

There are about 500-1000 home runs per grouping, which leaves it prone to skewness. Albert Pujols and Adam Dunn were born two months apart and their tremendous power probably contributed to the large break between ages 28-29 and 29-30.

Next up I graphed standard distance against a batter's weight. It’s a standard assumption that heavier players have more raw power. And even though listed player weights are some of the more unreliable baseball data available, the relationship is still undeniable.

Less obvious is the relationship between home run distance and batter height. Yet the trend is just as distinct.

When it comes to raw power, short players are at a greater disadvantage than light players while heavy players are at a greater advantage than tall players.

All of our assumptions about quantifiable measures that contribute to a batter’s power seem to hold true. Age, height, and weight are important in determining power. With pitch f/x data, we can also see what effects pitchers have on home run distance. This is getting into Defensive Independent Pitching Statistics theory. Max Marchi wrote a couple of great articles combining hit location and pitch f/x data. A good chunk of gameday data from 2007 did not have pitch f/x data, so I am working with closer to 7,000 home runs.

One would think that pitch velocity plays a part in determining how hard a ball is hit. To compare apples to apples, I used Hit Tracker’s speed off bat measure instead of standard distance.

It looks to me like pitch velocity is insignificant. Perhaps on the slowest of pitches, the ball doesn’t receive the same force off the bat, but every group faster than 80 miles per hour generates a speed off bat within half a mile per hour of each other. That’s nothing.

I wanted to see if there were any balls that left the pitcher’s hand with a greater velocity than that which they flew off the bat. There were about a dozen cases, with the biggest disparity in velocity coming on a 345-foot, 96 mile per hour Carlos Pena homer off a 99 mile per hour A.J. Burnett fastball.

Now, if I were Dave Allen I would come up with some awesome heat charts to demonstrate the relationship between pitch location and standard distance. I am not. But I do have bar charts. Here is pitch height plotted against standard distance.

I’m 6’2” and the top of my knee is exactly two feet high. Meanwhile, the top of my belt would be 3.5 feet high, but there just aren’t that many homers hit in the top layer of the strike zone. It would appear that home runs are hit the farthest on pitches at or around the knees. I’m not a physicist, or a physician for that matter, but I believe there are two factors a batter can control in how far he hits the ball: force and trajectory. I decided to break these down by pitch height.

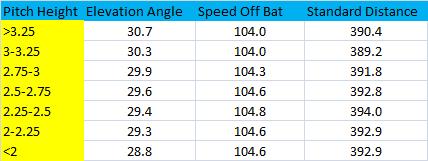
Batters hit the ball hardest on pitches down in the zone. But the elevation angle—which is defined by Hit Tracker as the angle above horizontal at which the ball left the bat, in degrees—might actually determine why balls fly farther when batters go down to get them. The increase In elevation angle is uniform, and in general the lower the elevation angle, the higher the home run distance. The correlation coefficient between the terms is -.25. Furthermore, there is a correlation coefficient of -.5 between elevation angle and speed off bat, which affirms that batters want to get on top of the ball, so to speak. Of course, the reason for the negative correlation between home run distance and pitch height could actually be the horizontal launch angle. Maybe low pitches are easier to turn on than higher pitches.

I broke down horizontal pitch location by batter handedness.

This is from the batter’s perspective, so pitches 2-6 inches from the center of the plate (on the right) are outside to right-handed batters.

I’m extremely surprised to see that batters hit pitches outside farther than they hit pitches inside.

I incorporated pitcher handedness as well as home run field location to find the differences in platoon splits.

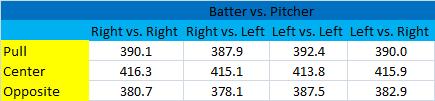
Lefties not only hit longer homers on outside pitches than righties, but they also hit longer opposite-field home runs. These two points are probably intertwined. Other than that, I don’t see anything notable in platoon splits.

Finally, I looked at the count’s effect on home run distance. I might have saved the best for last, as there is quite a clear relationship, which strongly signifies a change in hitter approach.

On 3-0, hitters get better pitches to hit and might even swing harder when they choose to let it fly, and with two strikes hitters get worse pitches to hit and might shorten their swing to protect the plate. Again, this is selective sampling. Batters will only hit home runs on decent pitches. And pitchers are even more likely to throw fastballs over the heart of the plate when behind in the count than they are when ahead.

Thanks to Greg Rybarczyk and MLB for making all this wonderful data freely available.