
| Crunching the Numbers | December 07, 2009 |
I just wanted to post a short follow-up to a post from a few days back, Controlling the Zone in order to make what might appear to be a completely unreasonable assertion. Those are, after all, the best kind.
Umpires absolutely should be biased to give pitchers with good control a wider strike-zone. If an umpire does not give a pitcher with good control a wider strike zone, then he is being unfair.
The basic principle is this: if a pitcher has better control, then before you even see the pitch you should guess it will be a strike. If you see a borderline pitch that could go either way, you will be correct more often if you err on the side of calling strikes. That may not be too convincing, so let's do better.
Let's simplify this and look only at the lateral location of the pitch. Figure 1 shows a hypothetical distribution of pitches for a given pitcher. We'll assume that the distribution is normal along this dimension (this assumption is false for real pitchers, but that doesn't matter for our purposes here). In blue, we see the majority of pitches (60%) that fall between -10 and 10 inches from the center of the plate. These pitches are "true" strikes; they actually crossed the plate. The area in red represents the 40% of the pitches that fall outside the zone. These are "true" balls.
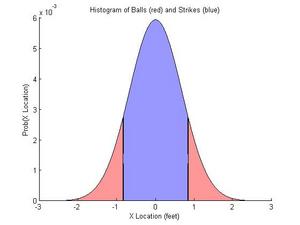
Figure 1. Histogram of "True" balls and strikes
Now let's assume that the umpire doesn't have direct access to the "true" location. Instead, he perceives the location of the pitch, but his perception has some uncertainty in it. Let's assume that the umpire will perceive the location of the pitch to equal the true location plus or minus a normally distributed error term. If we take the red distribution from figure 1 and convolve it with a Gaussian error term, we get the green distribution in figure 2. This green distribution represents where the umpire will perceive all of the "true" balls to cross the plane of the plate.
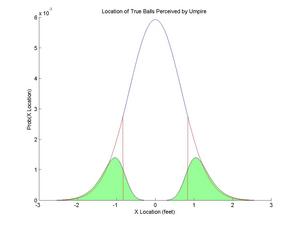
Figure 2. Histogram of the perceived location of "true" balls
Of these true balls, many appear to the umpire to cross the plate in the strike zone. That is, just the fact that the umpire is not perfect leads to some misclassifications. The green area in figure 3 reflects the true balls that are called strikes. In this figure, 16% of the actual balls are called strikes because of this error. But this isn't a bias; this error term will apply to all pitchers, regardless of their skill level.
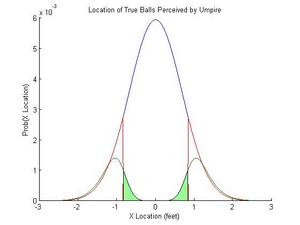
Figure 3. Pitches misclassified as strikes
The bias in the umpires perception comes in if he is trying to maximize his own performance, that is, make the fewest mistakes. The perceived distribution of pitches in figure 2 and 3 show how they would be classified if they were each considered in isolation. But we have a lot more information: we know the overall distribution of pitches. We know that a pitch closer to the center of the plate is more likely than a pitch outside. Therefore, our optimal guess, given the information and uncertainty that we have, is shown in figure 4. The green distribution in figure 4 shows the perceived location of the actual balls after the umpire takes his prior knowledge into account.
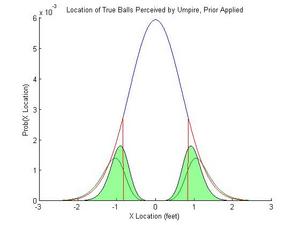
Figure 4. Pitches misclassified as strikes
Nearly 40% of the "true" pitches are now being classified as strikes (that's OK, some of the strikes are going to be misclassified as balls). Figure 5 shows the source of the misclassification. The area in red is the error caused by measurement error, the noise in the umpires perceptual system that causes him to be inherently uncertain. The area in green is caused by his priors, which will change depending on the context. If he faces a good pitcher with great control, the umpire's prior distribution should be very tight, with many strikes. If he faces Joel Zumaya, the umpire's prior distribution should be much more even (or even inverted, so that he is biased to call a ball).
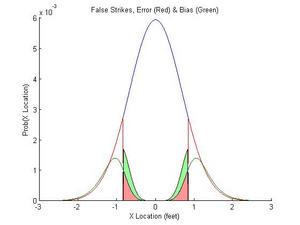
Figure 5. Pitches misclassified as strikes
Failing to take the context into account will result in impaired performance. The umpire would get more pitches wrong. If an umpire takes this "bias" into account, he is actually being as fair as he can be. If he did not use this bias, he would actually be unfairly biased against the pitchers with better control. What is fairness? Here, we would want the umpire to mistakenly call a true ball a strike as often as he calls a true strike a ball. If the umpire does not update and apply a prior based on the context, he is being unfair by this definition: when judging a good control pitcher, he will misclassify more true strikes as balls than vise versa.
Hence my initial claim: Umpires absolutely should be biased to give control pitchers a larger strike-zone.
This might be able to explain why the strikezone is a
All of that said, it's entirely unclear how an umpire should construct his prior, or what experiences should be used as a basis. Should it be based on a pitchers history? History with that umpire? The performance of that pitcher that day? The performance of all pitchers that day (not too unreasonable if the process is automatic)? The hypothesis becomes hard to test because the prior could be constructed in a number of very different ways.
Comments
I have done a lot of officiating in a lot of sports, and to me, the easiest task is calling balls and strikes (which IMO is much easier than, say, tag plays).
An umpire draws an imaginary picture tube which is the strike zone as he sees it. The pitch either breakes that picture tube with at least one stitch or it doesn't.
That's not to say even the best umpire doesn't miss pitches. He does. But he shouldn't miss them because he gives the close ones to the pitcher with good control or doesn't give them to the pitcher with poor control.
That said, we are nearly all creatures of habit. I suppose that subconsciously it is easier to call a pitch a strike when one has been calling strike after strike, and vice versa with balls.
And no doubt whether the pitcher has good control or the batter a good eye can likely also enter the equation at a subconscious level.
But I have found the best way to call a ball or a strike is to think about whether the pitch broke the picture tube or not, then see how my gut feels about the call I am about to make. If my gut likes the call (which it does a very high percentage of the time), I go with the call. If my gut doesn't like it, I usually go with my gut.
While even most sports officials are human (as opposed to being zebra-like or "blue"), I think it is a mistake to change one's strike zone in any way based on the pitcher or the hitter -- with one exception.
Obviously one should adjust the strike zone to where-the-catcher-catches-the-ball equation based on the movement of each pitch, and one should adjust his strike zone based on the height of the strike zone based on where the hitter stands when he his swinging at the pitch.
Otherwise, the strike zone should be identical for each batter and each pitcher. Isn't that the way the rule book is written?
Posted by: SharksRog at December 7, 2009 3:55 PM
Hi SharksRog,
I'm not surprised that you're skeptical. But in your comments, you are really describing two very different methods for calling pitches. You have described a rule-based, conscious "picture tube" system, and a subconscious "gut feeling" system. And it sounds like your gut usually wins when there's a discrepancy.
Your visual system simply isn't good enough to have 100% certainty whether the ball caught the plate. Some pitches will be obvious to you. But there will be pitches that your "picture tube" system will say the chances it crossed the plate are 50-50. What do you do then? If your optimal, you call it a strike more often than not. I'd argue that your gut-based system is doing this processing without your knowing it.
Neuroscientists are finding evidence for this type of Bayesian processing in the most basic of behaviors, all of which are unconscious. Hitting a tennis ball, for instance, requires Bayesian inference (there are some very cool studies to show things like this), but if you ask a tennis player if he is biased by perceptual cues, he would say "No, I just hit the ball."
The nuts and bolts of how your brain makes these decisions requires these types of inferences and biases. I'd say that your conscious (picture-tube) system is at best used to confirm your gut feeling; at worst, it is your way of understanding why you did what you did, without it really having any true effect on your decision making.
Convincing? Or not at all? :)
Posted by: cdm at December 7, 2009 5:10 PM
Just a quick link to a presentation of some interesting psychological work on Bayesian inference and motor planning.
http://www.eucognition.org/euCognition_2006-2008/six_monthly_meeting_5/Daniel_Wolpert_presentation.pdf
Posted by: cdm at December 7, 2009 5:45 PM
Hey, Chris. Thanks for your response.
You know a whole lot more about the science of this than I do, so my guess is that you're right in all you say -- with one possible exception, which may be merely semantics.
My initial ball/strike call -- which is made mentally after I have watched the pitch into the catcher's glove -- is almost entirely a visual process (as far as I am consciously aware, at least). I am essentially basing that call on a picture.
My gut feeling likely includes a broader input, including the sound of the ball hitting the mitt. You know the old saying, "It SOUNDED like a strike?" There is some truth to that, although with a curve ball in particular it is possible for the sound to be incorrect if the catcher catches the pitch just right.
Anyway, my gut feeling comes into play (again, at a conscious level) AFTER I have mentally made my call based primarily on what I saw. If that gut feeling is knawing enough, I will change that mental call. That often doesn't happen at all and usually no more than once or twice during a game.
To me, calling a basketball game is far more difficult, since it requires assessing advantage and disadvantage as well as degree of contact. In fact, while the decisions I made as a CFO were obviously far more important from a financial standpoint, I often felt the decisions I made as a basketball ref were more difficult -- since they had to be made almost instantaneously rather than after detailed analysis.
Similarly, in baseball, tag plays are the hardest. IMO one mistake umpires sometimes make is being TOO close to the play. If one is too close, it can be almost impossible to see both the hand or foot touching the bag and the tag on the body simultaneously. And if an umpire can't do that, he winds up making an educated guess.
Another difficult thing about tag plays is that it isn't always possible to acquire the best angle from which to view the play. And almost any sports official will tell us that having the angle is more important than being close to the play.
A final difficulty on tag plays is that the umpire needs to watch the ball for quite a while to ensure he doesn't interfere with the play or get hit with the throw. That can result in a quick eye movement to the play, which no doubt makes focusing difficult.
But on balls and strikes, the umpire need worry only about the strike zone. His peripheral vision can usually take care of balls hit off a batter's body or a pitch grazing the batter's shirt.
Speaking of balls hit off a batter's body, I'm not sure I have ever seen a direct call made on that from any umpire other than the home plate umpire. That is often an easier call by one of the base umpires, and I was taught to raise my hands as a base umpire and yell "dead ball" if I saw a batted ball hit the batter's body.
One thing I like is that umpires are communicating more on calls. Since angle is the most important factor, the umpire closest to the play and who has primary responsibility for the call isn't always the umpire with the best angle.
To me, it's not important WHICH official makes the call. What is important is getting that call right.
Posted by: SharksRog at December 8, 2009 10:50 AM
Umpires absolutely should be biased to give control pitchers a larger strike-zone.
Most ludicrous suggestion about baseball I've ever read.
Posted by: El at December 9, 2009 7:03 AM
El, thanks for reading a sentence of the article before voicing your opinions. One of the nice things about the Saber community is their willingness to consider new views that contradict their intuitions. I'm glad you gave it a chance.
Posted by: cdm at December 9, 2009 8:15 AM
Great work Chris,
I've never seen this approach - but I have seen the argument for bias towards control before: Tom Glavine's book - Living in the Black, I think it's called, touches on this.
Baseball is about stats and neverending arguments about the DH, wild cards and pitch counts. Thanks for continuing the legacy!
Posted by: Nathan at December 9, 2009 10:45 AM
This is great. I do the same stuff in astronomy all the time. It's great to procrastinate from my work to see it applied to my distraction (sports). Keep up the great thought-provoking work!
Of course, a real pitchers distribution is far from normal (Gaussian), but the main point remains: if the pitcher throws a different amount of "real" strikes within the measurement error of the zone border than "real" balls in the same spatial range, a bias will exist.
Just discovered the site, so i'm looking forward to finding more of this level of analysis!
Posted by: Zod at December 9, 2009 11:03 AM
Really good stuff. Well said.
Posted by: Phil Birnbaum at December 9, 2009 11:06 AM
El, when you read a book, (maybe that is even a stretch) do you decide after the 1st sentence whether or not the entire book sucks?
Posted by: Brendan at December 9, 2009 11:38 AM
I like this analysis and the approach, but I think the problem is actually a lot more challenging than it is made to seem. The main problem is not so much that the distribution is Gaussian, but rather that it is centered around the the center of the strike zone. Pitchers may not be aiming to pitch strikes every pitch; they're trying to get people to strike out, which is entirely different.
Second, if pitchers know that umpires are using their priors on pitchers' control to evaluate strikes and balls, the pitchers are going to change their behaviors as well, again distorting the distribution of the pitch location to maximize their probability of getting an out.
The intersection of the umpires' and pitchers' decisions makes for game that may be challenging to solve with some really weird looking and very intractable equilibria.
Posted by: Jon at December 9, 2009 8:23 PM
Instead millions of people writing their math thesis on perceived balls and strikes with lots of assumptions, why not sensor up the plate, computerize everyone's measurements and send the home plate umpire to the showers. You would then never have a true ball called a strike or a true strike called a ball. I think the playoffs showed that these guys are Far from perfect and the more judgement you can take from fatty the better. You could
actually leave him there and when the batter steps in and the pitcher gets set the ump could enable the sensors. They do it in tennis, its time now for the plate to be automatic.
That part of the game is almost as bad as the NBA biases.
Why should a pitcher have to EARN a strike zone? When Larry Bryd and Magic came into the league they didnt have to earn the baseket width.
Posted by: PaulGT3 at December 9, 2009 8:28 PM
Instead millions of people writing their math thesis on perceived balls and strikes with lots of assumptions, why not sensor up the plate, computerize everyone's measurements and send the home plate umpire to the showers. You would then never have a true ball called a strike or a true strike called a ball. I think the playoffs showed that these guys are Far from perfect and the more judgement you can take from fatty the better. You could
actually leave him there and when the batter steps in and the pitcher gets set the ump could enable the sensors. They do it in tennis, its time now for the plate to be automatic.
That part of the game is almost as bad as the NBA biases.
Why should a pitcher have to EARN a strike zone? When Larry Bryd and Magic came into the league they didnt have to earn the baseket width.
Posted by: PaulGT3 at December 9, 2009 8:28 PM
@ PaulGT3
You're right about the accuracy of systems like Questec, but this is one area where "tradition" (having human umps) is likely going to trump technology for the foreseeable future.
From what I have heard though, pitchers like Glavine hated the Questec because the umpires were judged on their accuracy and therefore weren't giving them the borderline calls that they previously got on reputation.
As for NBA stars, its true that they don't earn bigger baskets, but they do often get favorable calls from officials. And I seriously doubt that "millions" of math theses are getting written, let alone about baseball. If it was the case, so much the better! I'm all for more statistical education.
Posted by: Steve at December 9, 2009 10:09 PM
So this whole premise is based from an admittedly false assumption that a pitcher hits the strike zone in a normal distribution? And then the pitcher hits the corner of the strike zone within a Gaussian error term?
Cause if that is true, then this whole premise is based off of nothing that actually represents real game scenarios. As we all know, pitchers have specific styles and will have different distributions accordingly. I doubt they can be reasonably modeled with a normal distribution across the plate. Maybe there could be some analysis of real life data before we throw out these definitive statements that support stereotyping specific pitchers.
As we see many times in real life, theories are only as good as the assumptions they are built upon.
Posted by: chase at December 9, 2009 11:25 PM
Thanks for the comments. We seem to have the full spectrum of opinion here, from "ludicrous" to "great". I'll go with the wisdom of the crowds and average that out to "of moderate interest." :)
Regarding Glavine, the point of this bias is not to give more credit than is due. An umpire biased in this way would give a pitcher the same percent of balls/strikes as a perfect computerized system. Glavine doesn't benefit from the bias in officials, he just doesn't suffer for it (at least, not for this reason).
Chase, you've made a logical fallacy here. As I mentioned in the article, I made the simplifying assumption that the pitch distribution is normal. I commented that although this assumption is false, the violation of this assumption does not change the outcome of the analysis. The only assumption under which the conclusions are wrong is a flat prior (e.g., the probability of throwing 1 foot outside the zone is the same as in the center). Under *any* non-flat true pitch distribution, these conclusions hold. No pitcher has a flat distribution.
Posted by: cdm at December 10, 2009 6:15 AM
I read the entire article before posting and I agree with Jon;
the more judgment you can take from [the HP ump] the better
Accurately determining where the ball passed thru a certain space 6-5 feet in front of him, rather than at 7 or 4 feet in front is not humanly possible, and every pitch called wrong dramatically changes the AB and thus the game.
Sorry, but your idea does nothing to fix the problem.
Posted by: El at December 10, 2009 6:42 AM
Appreciate the effort, but as a lawyer interested in justice rather than a mathematician, I disagree with your idea of fairness. You posit that getting the most calls right is the most fair way of calling the game. I disagree. In any situation, a court or a field, equal treatment is highest principle. Yes, the control pitcher may be on the bad end of missed calls more often than a wild pitcher, but since both of those entities (control and wild pitcher) are subjective and given to change at the whim of the home plate ump, the highest level of fair you can offer a control pitcher is that his pitches are being called like the every other pitcher.
Posted by: JD at December 10, 2009 7:17 AM
It seems like on many close calls the good control pitcher is actually aiming to throw a ball. how should the umpire adjust for this? should he make assumptions based not only on the pitcher but also on the count and other game situations?
Posted by: matt at December 10, 2009 8:01 AM
Yeah, Matt gets close to the issue. You jumped straight into quantitative analysis without doing anywhere near the amount of qualitative analysis necessary to set up the problem.
So while I agree with your approach in the trivial case (in which the pitcher is trying to throw a strike down the middle), you actually need a much fuller set of priors to allow the umpire to accurately use Bayesian reasoning here.
For example:
1. What are the odds that Tom Glavine misses the strike zone on an 0-2 count? When he is aiming close to the strike zone, presumably he will miss more often than Joel Zumaya, when Zumaya is also trying to barely miss the strike zone.
2. Is a pitch by Tom Glavine more likely to be a ball, since he knows the umpire is giving him a strong benefit of the doubt? In this case he far more likely to be aiming at a point a couple inches off the edge than down the middle, so he's more likely to have thrown a ball on a close pitch than a worse pitcher.
There's strong evidence that case 2 is an accurate description of what was going on in the mid-90s with Glavine and Maddux (and Livan Hernandez for one glorious day). The point being that creating priors without taking into account the new equilibriums created by umpires using those priors is overly simplistic, and also creates worse outcomes (in terms of correct calls).
Posted by: Tim at December 10, 2009 11:11 AM
The biggest flaw I see in the analysis was brought up earlier, but not addressed in the comments - that you are assuming that a pitcher is ALWAYS TRYING TO THROW STRIKES.
To take it a step farther, you're normal distribution is centered on the center of the plate - wouldn't each pitch thrown have its own center of distribution? Say, if a pitcher is trying to hit the outside corner, the high point of the distribution FOR THAT PITCH would be centered on the outside of the plate. A more accurate pitcher will have a narrower distribution there than a "wilder" hurler for that same pitch, but in order to judge that, the ump needs to know which pitch the pitcher was trying to throw.
Thought-provoking analysis, and very interesting to read, though. Thanks.
Posted by: Sean at December 10, 2009 11:12 AM
Sean,
Not quite true. I am assuming that the pitches are sampled from the same distribution. It is true for all pitchers (of note) that, in aggregate, they throw more strikes than balls. If we stipulate that we know nothing about the pitchers strategy, we will assume that stationary distribution. Using that distribution, the umpire should be biased in favor of a control pitcher.
But as Tim alluded to, a prior can be constructed in many ways, and it is unclear what information the umpire will take into account. For instance, if it is a 0-2 count, this information may change the distribution, making his prior different.
So for each situation, the umpire constructs a prior. If the probability of a strike is greater than the probability of a ball under this prior distribution, the pitcher should be biased in favor of control pitchers.
Alternatively, it could be that in a 0-2 count, the pitches that Tom Glavine places near the edge of the zone are more likely to be balls than strikes. In this case, if the umpire used this distribution as a prior, he would be biased against him, like he would be biased against Zumaya.
I do not believe there is any pitcher (with the possible exception of Mariano Rivera) who has control so good that pitches near the edge of the zone are more likely to be balls than strikes. But I fully concede that if an umpire used that as his prior, the bias would be reversed.
Posted by: cdm at December 10, 2009 11:32 AM
I do not believe there is any pitcher (with the possible exception of Mariano Rivera) who has control so good that pitches near the edge of the zone are more likely to be balls than strikes. But I fully concede that if an umpire used that as his prior, the bias would be reversed.
Fair enough. The main issue here is that this is a dynamic system that is constantly updating, with everyone looking for an exploit.
The pitcher is trying to see if the umpire is giving him the benefit of the doubt, and adjusting accordingly. Clearly the umpire should update his prior at that point, since a perceived ball from a control pitcher who knows that the umpire will give him the benefit of the doubt was more likely to be a ball. If the umpire does not adjust here, his strikezone becomes exploitable.
(of course we quickly get into Princess Bride territory at this point, where the umpire knows that the pitcher knows that the umpire knows what he's doing, and he can clearly not choose the wine in front of me)
And again, the mid-90s Braves example shows how the umpire's prior was exploited over a long period of time.
To draw an analogy: for the umpire to use a simple "good control = more likely to be strike" prior is similar to a poker player who goes allin every time he has Jacks or better, because it's ahead of what other players probably have. Yes he is ahead, but he is not taking into account the fact that other players dynamically update their information, and will soon exploit this by only calling him with better hands.
Similarly the umpire in your argument does not take into account that he is a part of the system in creating his priors.
Does this mean that using Bayesian reasoning to call balls and strikes is a bad idea? NO! It just means that you need richer priors (no pun intended, and I don't even know what I'd do with the pun if I intended it).
For example, you could give Curt Schilling the benefit of the doubt, since he showed a "throw it down the middle" approach in his career. But you would want to continuously check players Questec stats to see what their locational biases were in certain counts, and if they were adjusting over time.
Point is that it's a non-trivial problem, and a simple heuristic like the one you propose would probably only work in the short term, before being heavily exploited at the margin.
The most obvious exploit I can think of is that control pitchers would start to aim slightly farther to the corners, since they would keep the same amount of strikes, but on average have the ball in harder locations for hitters to hit.
Now, if you used Questec on a frequent basis, and updated your priors so that you no longer classified them as control pitchers, your reasoning would hold.
Posted by: Tim at December 10, 2009 12:13 PM
Your analysis is extremely interesting, but you make some false assumptions about the concepts in your model. Most of these have been pointed out a above, but I'd like to clarify them further in the interest of reaching a more refined analysis at some point.
First, you seem to assume that control is the same as location. It is not. A pitcher must control the velocity, release point, and curvature of a pitch in addition to the location over the plate. I think location over the plate is the variable you are interested in, not control. Use of the normal prior assuming more pitches located in the strike zone seems to support this. In order to really articulate this analysis it would be helpful to study the extent to which the velocity, release point, and curvature of a pitch relate to the location over the plate.
While pitchers with the best control have the capability of placing every pitch in the strike zone, they would be foolish to do so. It is important to know the tendencies of the batter and use plate location that is most likely to get an out. Sometimes this means the strike zone, but not always.
You also seem to assume that the batter and the umpire infer from a rating of the pitcher's location control whether the ball will be a strike or not. This is probably not the case either. Depending on the count and the game situation, the batter will look for various properties of a pitch in order to determine not only whether to swing, but the type of swing to use (swing for the fences, tap into right field etc).
Swinging complicates things for the umpire's inference as well. In the construction of the assumed normal prior all swings are strikes regardless of the location of the ball over the plate. Swinging and missing implies good control on the part of the pitcher, but a batter can swing and miss at a pitch because it is outside the strike zone or because the velocity is high or low and the swing is timed incorrectly. Also, a foul ball that is inches from being a home run is also recorded as a strike.
I think there may be a helpful hint in your last reply post from earlier today. Focusing only on the distributions of pitches at the edge of the strike zone would seem to relax some of the problems with assumptions regarding the pitcher's intended target (ie manager says throw to the glove and the glove is outside the zone) and the use of a normal prior.
Given the overall sophistication of your analysis, your design could be improved by using something better than "pitchers throw more strikes than balls" for the distributional assumption.
With very large samples it is unlikely that the selection of a prior would have a large effect on any statistical analysis. However, you have presented a more theoretical model that doesn't seem to manipulate actual balls and strikes data collected from ballplayers. Using data made available from MLB, I think it would be possible to do this and you could then conduct a sensitivity analysis which would refute concerns about selection of a prior. The mlb data also includes velocity, trajectory and release point in addition to plate location.
Posted by: Adam at December 10, 2009 12:50 PM
I'm new to the site, but intrigued by the post. As a Bayesian statistician and psychometrician, I'm always thrilled to see Bayesian inference applied. That said, I'm not sure I agree with the conclusion. Several previous comments have questioned the distinction between location and control, intent of the pitcher, and taking the count into consideration. In Bayesian terms, it's not clear that all pitches should be considered exchangeable, as is essentially done in the analysis. Moreover, the issue of fairness is key.
That said, I'm not sure I'm quite convinced by this. If the issue is as they say. You argue:
"What is fairness? Here, we would want the umpire to mistakenly call a true ball a strike as often as he calls a true strike a ball."
But I don't think when we say we want an umpire to be fair that's what we mean. As JD commented earler:
"...I disagree with your idea of fairness. You posit that getting the most calls right is the most fair way of calling the game. I disagree. In any situation, a court or a field, equal treatment is highest principle..."
There is a direct analogy here to educational assessment and testing, where the pitchers are the examinees, the pitches are the observations on the test (i.e., answers to questions) and the umpire is the scoring mechanism.
By the same reasoning advanced here we may say in educational testing "if I incorporate prior information about examinees, I'll get more accurate estimates of their proficiency." However, this gets dicey. Suppose a test administrator believes (as many people do) that males are better at math than females. An implication of following the logic advanced above is that, for a male and female examinee who produce the same responses on a test (i.e., loosely speaking answer all the same items with the same answers), our estimate of the male's math proficiency should be higher than that of a the female's math proficiency. Is that fair? Probably not by way of what we typically mean by fair. This is a well-known tradeoff between estimating examinee proficiencies' accurately and fairly. As a field, the assessment community has chosen to maintain fairness, especially in high-stakes assessment environments. To flesh out the analogy, the umpire (test/scoring algorithm) should treat all pitchers (examinees) fairly, in the sense that the same pitches (answers on the test) should be evaluated the same (allowing for umpire measurement error) without regard to who the pitcher (examinee) is.
Posted by: Roy at December 10, 2009 1:29 PM
My apologies for the grammatical errors in the previous comment. Copy/paste + sporadic connection = sloppy text. Hopefully the point is still clear.
Posted by: Roy at December 10, 2009 1:38 PM
i read the whole article and i agree with one poster:
it is a cute try, but ultimately, this is one of the articles that does a great disservice to sabremetrics. publishing papers is good because there is rigor. publishing on a blog is irresponsible because you commit disinformation without edit.
as described in many of these posts, you bring up an interesting argument, but you assumptions are totally invalid, and you cannot reasonably agree with your initial argument based on this analysis.
a nice effort, but you are only spreading wrong information.
this is like saying, "i studied 40 children that got the flu shot and 5 of them developed autism" and then concluding "don't get the flu shot because it causes autism."
i've read your other works, and you are much better than this. don't go for the cheap headline to get more traffic (although, admittedly, the cheap headline worked on getting me to the site).
i do enjoy most (>80%) of what's on the site though.
Posted by: ed at December 10, 2009 2:04 PM
Another question this begs to be asked is the concept of fairness. Is being unbiased the most important part of umpiring? This analysis explicitly suggests that calling actual strikes as balls is okay, as long as there are enough missed calls in the other direction to counteract these mistakes. I would argue that the umpire's goals is to minimize the number of actual errors, on a pitch-by-pitch basis, rather than the errors in the aggregates. With this methodology you may end up with a number of called strikes pretty close to the number of actual strikes, and a number of called balls pretty close to the number of actual balls, but a high number of errors on specific pitches.
Posted by: Ben at December 10, 2009 2:32 PM
Yikes, now I'm doing a disservice to sabermetrics. No one tell Rich Lederer! :)
The question of fairness is an interesting one. Roy, you're 100% right. I can't say what's fair in educational testing. But I do know that my car insurance is higher because I'm male. The money coming in from policy holders needs to balance out the money being paid in claims. If they didn't charge men more, despite men making more claims, they would essentially be overcharging women and undercharging men. So even though I'm a driver, I get charged more. Is that fair? I don't know.
I'll steer clear of making strong claims about fairness, and back off to some solid ground: fair or otherwise, a biased umpire will make fewer errors over the course of a season. If that's how you evaluate an umpire, then a biased umpire is a good umpire.
Posted by: cdm at December 10, 2009 3:29 PM