
| F/X Visualizations | April 06, 2009 |
In my previous posts I have averaged over all counts, but intuitively and empirically we know that pitchers and batters behave differently in different counts: Joe Sheehan showed that pitch location and batter's swing rates, John Walsh that pitch type frequency and Jonathan Hale that the size of the called strike zone all vary by pitch count. In this post I build on, combine, and present in a visual manner some of these previous results.
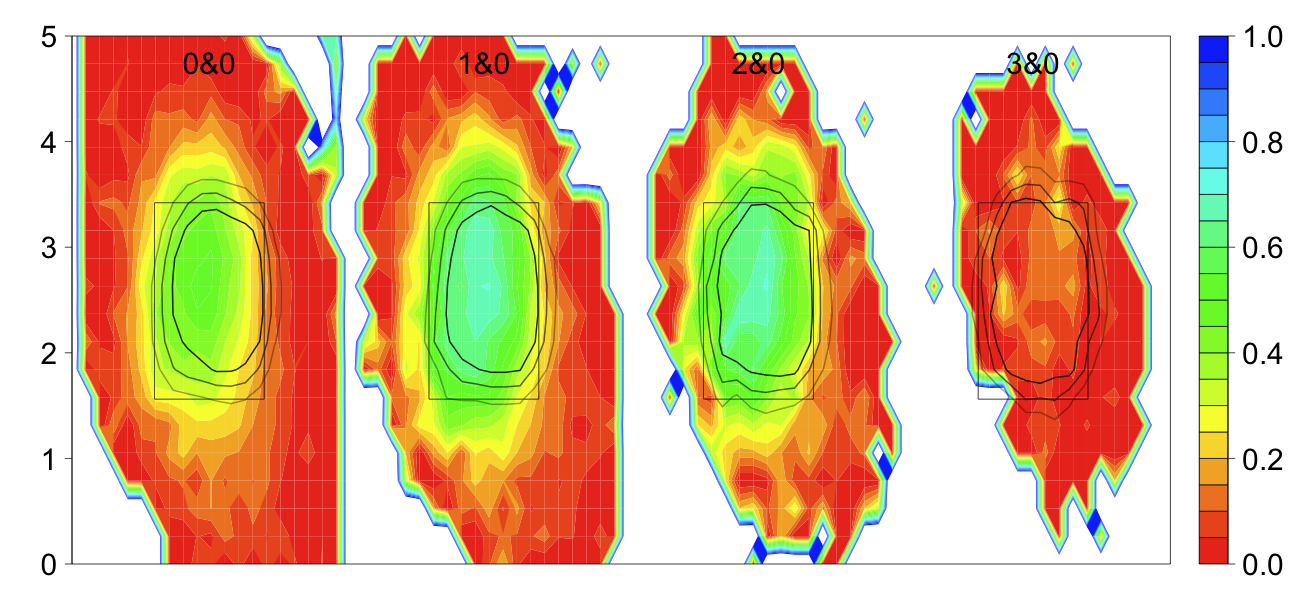
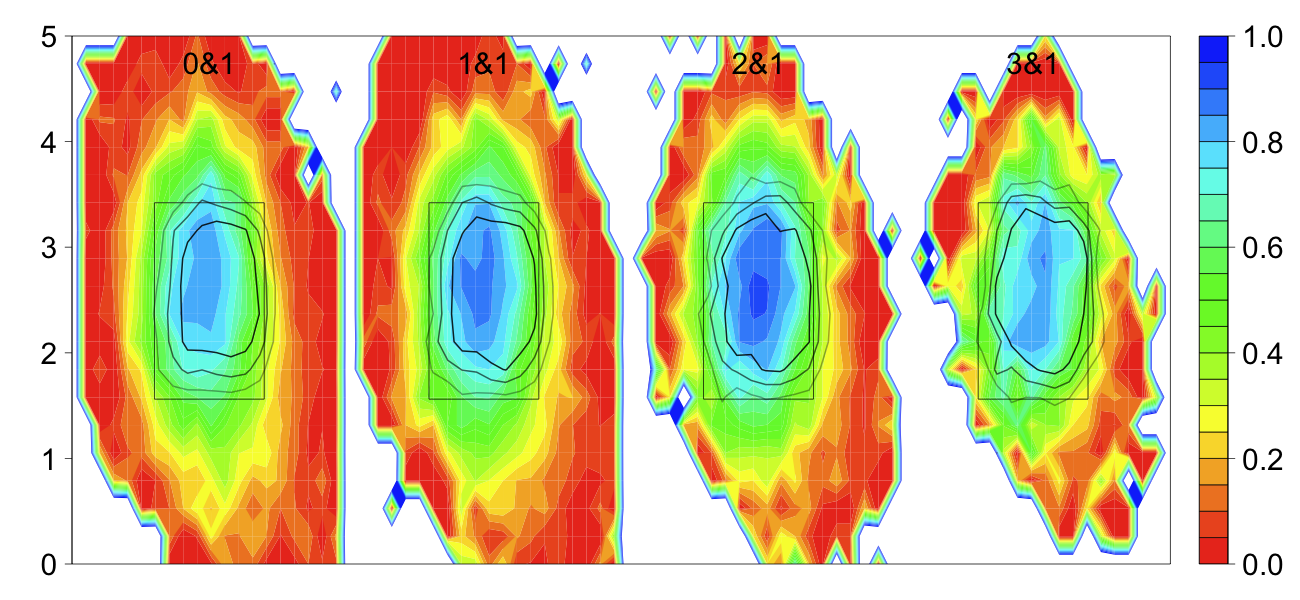
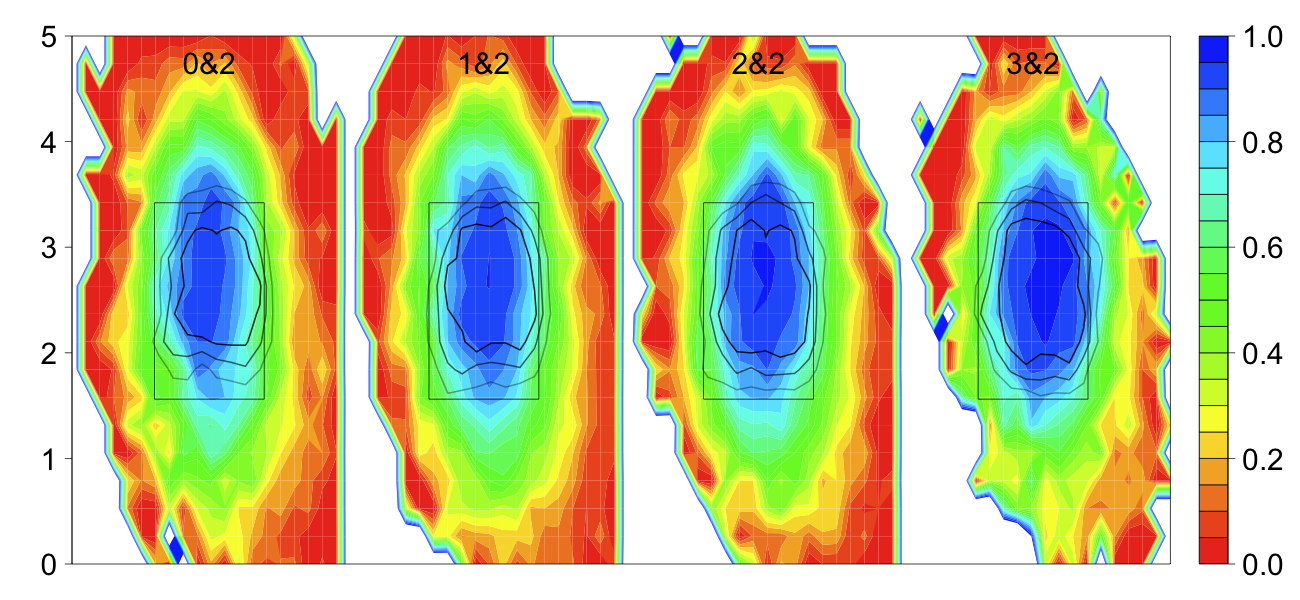
Below I reproduce the first panel from my deconstructing the run value map posts, but here separated by count and averaged over pitch types. The heat map is the batter swing rate, the percentage of pitches in a given location the batter swings at. Over that are the 25%, 50% and 75% strike contours for taken pitches. This means taken pitches inside the smallest contour are called strikes over 75% of the time, pitches between the smallest and middle contours are called strikes between 75% and 50% of the time and so on. The strike zone is called differently to RHBs and LHBs, so I restricted this analysis to just RHBs.
Swing Rate
Batters swing more when there are most strikes (going down a column). In favorable counts batters swing slightly more inside, but that tendecy is lost in pitcher's counts. In order to see the trends in swing rate better I averaged over all locations in and out of the strike zone (using the 50% strike contour not the rule book zone).
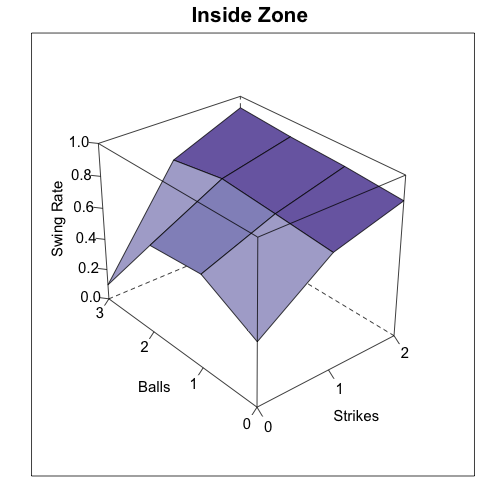
Swing rate inside the zone +-----------+---------+---------+---------+---------+ | | 0 Balls | 1 Ball | 2 Balls | 3 Balls | +-----------+---------+---------+---------+---------+ | 0 Strikes | 0.405 | 0.587 | 0 .559 | 0.096 | | 1 Strike | 0.727 | 0.762 | 0.795 | 0.742 | | 2 Strikes | 0.850 | 0.880 | 0.898 | 0.927 | +-----------+---------+---------+---------+---------+

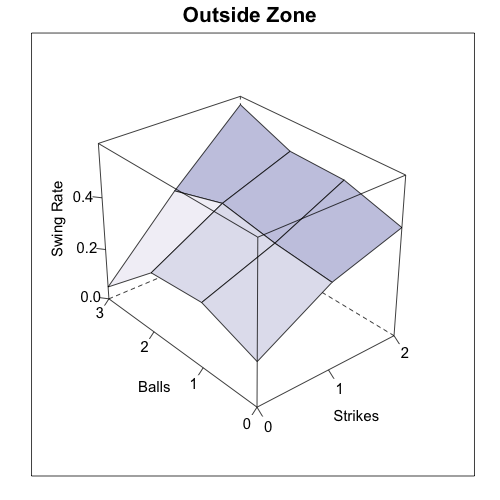
Swing rate outside the zone +-----------+---------+---------+---------+---------+ | | 0 Balls | 1 Ball | 2 Balls | 3 Balls | +-----------+---------+---------+---------+---------+ | 0 Strikes | 0.171 | 0.249 | 0.232 | 0.049 | | 1 Strike | 0.330 | 0.350 | 0.385 | 0.325 | | 2 Strikes | 0.414 | 0.478 | 0.484 | 0.568 | +-----------+---------+---------+---------+---------+

There is no uniformly increasing or decreasing swing rate trend with number of balls like there is with number of strikes. Batters swing at roughly the same rate with one and two balls, and less than that when they have zero or three balls. But the size of this effect is quite variable depending on the number of strikes. It is very pronounced with no strikes and quite small with one or two. Interestingly batters swing more in 3&2 counts than in 2&2 counts (or any other count for that matter), which runs counter to the above trend. Intuitively this seems like a mistake on the part of batters and it would be interesting to see if this is case, perhaps taking a game theoretic approach like iamawesomer recently did.
Strike Zone
The size the of strike zone changes dramatically in the way that Hale previously demonstrated. As the number of strikes increases the strike zone shrinks and as the number of balls increases the strike zone expands. One thing we can do here, beyond Hale's original analysis, is see where this expansion and contraction take place. As the number of balls increase the top of the strike zone gets higher and the bottom lower, but the outside and inside edge do not change very much. As the number of strikes increase there is some small movement of the inside edge in, but most of the change is the top moving down and the bottom moving up. So most of the change is a vertical, not horizontal, expansion or contraction of the zone.
In addition this analysis allows us to measure just how big the strike zone is in each count. The measurements below are in square feet. (In the image the strikes count in the opposite direction from the swing rate images.)
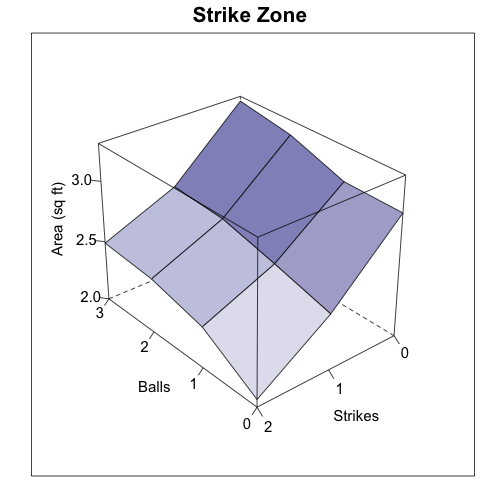
Area of the strike zone (sq ft) +-----------+---------+---------+---------+---------+ | | 0 Balls | 1 Ball | 2 Balls | 3 Balls | +-----------+---------+---------+---------+---------+ | 0 Strikes | 3.01 | 3.02 | 3.18 | 3.26 | | 1 Strike | 2.46 | 2.59 | 2.71 | 2.74 | | 2 Strikes | 2.06 | 2.34 | 2.45 | 2.49 | +-----------+---------+---------+---------+---------+

There is a substantial change; at its largest the strike zone is over 1.5 times the size of the zone at its smallest. But are these changes statistically significant? I noted in a past post that it seemed different pitch types were called differently, and we know that the frequency of pitch types thrown in different counts is different. So maybe the changes we see are an interaction of these two facts. For example 3-0 pitches are overwhelmingly fastballs, maybe umpires call a larger strike zone for fastballs than other pitches and the differences we see are not driven by count, but by pitch type.
To address this, and the overall significance of the zone size changes, I ran a binomial logistic regression. This is a regression in which the dependant variable only takes two values, in this case 1 if a taken pitch is called a strike and 0 if it is called a ball. The dependant variable is regressed against any number of ordinal and/or categorical variables. I regressed strike/ball against horizontal distance from middle of zone (in inches), vertical distance from middle of zone, the interaction of these two distances, length of pitch break (in inches), the number of strikes, the number of balls and the pitch type (the analysis uses fastballs as the baseline and compares the other pitches to them). I used x distance, y distance and x by y interaction rather than just distance so the strike zone isn't forced to be a circle.
Binomial Logistic Regression +-----------------+----------+------------+---------+------------+ | | Estimate | Std. Error | z Value | P(>|z|) | +-----------------+----------+------------+---------+------------+ | (Intercept) | 7.887 | 0.050 | 157.72 | < 2e-16 * | | x dist. | -0.570 | 0.003 | -163.49 | < 2e-16 * | | y dist. | -0.693 | 0.004 | -173.08 | < 2e-16 * | | x*y Interaction | 0.029 | 0.000 | 111.84 | < 2e-16 * | | Break | 0.027 | 0.005 | 5.51 | 3.6e-08 * | | Num. Strikes | -0.575 | 0.013 | -44.91 | < 2e-16 * | | Num. Balls | 0.213 | 0.010 | 21.76 | < 2e-16 * | | Changeups | 0.012 | 0.039 | 0.31 | 0.76 | | Curves | 0.037 | 0.049 | 0.77 | 0.44 | | Sliders | -0.038 | 0.026 | -1.43 | 0.15 | +-----------------+----------+------------+---------+------------+
So the effect of count is indeed significant. In fact, all else equal, each strike in the count decreases the likelihood of a pitch being called a strike the same amount as a pitch being one inch further away from the center of the zone (roughly equal estimates). The number of balls is also significant but the effect is less than half of that of the number of strikes (you can see in the image of strike zone area above, area decreases more as you increase strikes than it increases as you increase balls). The length of break is also significant, pitches with lots of break are slightly more likely to be called a strike. Once we control for break and count there is no significant difference in how the strike zone is called to different pitch types.
MLB is still interested in monitoring umpire performance and this year will replace QuesTec with a new Zone Evaluation system (which it seems is just the pitchf/x system). So I am sure MLB is aware, or will be aware soon, of the variable zone size based on count. I wonder if it is something they will try to change or if it is appreciated as being part of the fabric of the game.
Comments
Very nice. This is very useful info for pitcher analysis.
Re. the "new" umpire rating system, it is indeed nothing but PITCHf/x with some post hoc processing. They were actually doing it side-by-side in 2008, and, as early as May, MLBAM felt they were getting better data than Questec.
Posted by: Harry Pavlidis at April 6, 2009 6:22 AM
This is some neat stuff. I too find it curious that the swing rate on 2-strike pitches actually increases with the number of balls in the count. This seems like a possible indicator of a different mental approach dependent on the count, maybe some indicator of "will" to stay alive in an at-bat. Of course, trying to quantify "will" is like trying to quantify "clutch".
Posted by: Matt Mitchell at April 6, 2009 9:06 AM
Interesting analysis. Years back I came to believe that certain umps, (Chuck Meriwether was the most obvious) were much more reluctant to call strike three than they were to call strike one or two. Nice to see a degree of confirmation.
Posted by: James T at April 6, 2009 9:57 AM
It had always seemed to me that when the count was 0-2, that unless the pitcher threw the pitch right down the middle he would never get a called third strike.
I'm glad to see one of my many umpire aggravations is not just a figment of my imagination.
Posted by: Chris M at April 6, 2009 10:21 AM
Great, great stuff! I am more than a little skeptical of the swing rates on pitches outside of the zone. Swinging at more pitches at a 3-2 count than at a 2-2 count just seems implausible, as well as the .568 itself (can batters possible be swinging at so many bad pitches - balls - when they are 1 ball away from being walked?).
Dave in calculating those swing rates on balls outside of the strike zone at various counts, which strike zone did you use? The overall one (at all counts) or the one for that count only?
Another explanation for the smaller strike zone as the number of strikes increases is this (other than the umpire making a conscious decision to change his zone with the count):
When a batter takes a pitch with more strikes, he tends to be fooled by the pitch, either because he was expecting something other than what he got, or because of the pitch itself (a very big breaking curve, for example). The umpire will tend to be fooled as well. And of course, if a batter takes a borderline pitch with, say, an 0-2 count, the umpire often thinks, "It must have been a ball for the batter to take that pitch with 2 strikes..."
Posted by: MGL at April 6, 2009 10:43 AM
Very interesting analysis. I wonder if you would get a better fit using the square of the horizontal and vertical distance. It seems to me that a pitch right down the middle and one just one or two inches off the center of the zone would be called strikes with essentially equal probability (hopefully near one), while each inch nearer the edges would be increase in a non-linear way the likliehood of being called a ball.
Posted by: Gary H at April 6, 2009 1:18 PM
MGL,
For the swing rate in/out of the zone by count I used the 50% strike contour for that count, not the overall one, as the boundary. The higher swing rate at 3-2 than 2-2 is surprising, I think one reason is pitch type frequency. At 3-2 a fastball is much more likely than at 2-2 and batters swing at fastballs more often than other pitches. I should have broken up the analysis by pitch type.
I am not sure if there is anyway we could know, but I tend to agree with your suggestion that the change in strike zone size is not a conscious decision of the umpire.
Gary H. that is a good idea. I bet you are right that the probability based on distance is highly nonlinear.
Posted by: Dave at April 7, 2009 7:14 AM