
| Crunching the Numbers | October 22, 2009 |
There has been a lot of good discussion of pitch classification in the past, but recently few algorithms have broken into the saber-blogosphere. So I'd like to take the opportunity to propose a classification framework for identifying pitch types that is probably novel to most of the pitch F/X community. It isn't perfect, but I feel that it makes a good step forward, and hopefully it will turn the community on to some new methods.
Machine Learning & Classification
Pitch identification is a classification problem. There has been a ton of academic work in physics, applied math and computer science on classification algorithms. There are your regressions (vanilla, logistic, multivariate logistic, sparse logistic, least angle, ridge , kernel ridge, etc), k-nearest neighbor, k-means, support vector machines, neural networks, principle components, independent components, latent Dirichlet allocation, hierarchical Dirichlet processes, Bayes nets, etc (see MVPA or PyMVPA for good toolboxes designed to make large multivariate pattern classification analyses easier). Many of these methods haven't made it out of the fields they were first introduced to (e.g., genomics, topic modeling), but they have some interesting applications to MLB pitch identification. I'll describe a type of probabilistic model, a Bayes Net, and show how it can be applied here.
Hierarchical Probabilistic Models
A Bayes Net is a generative graphical model which makes explicit a hypothesis about how the data were generated. For instance, pitch F/X data may have been generated hierarchically like this:
1. A pitcher, p, is chosen
2. A pitch type, tp is chosen for that pitcher
3. Pitch properties, Xtp = {velocity, movement, location} are randomly sampled from a multivariate normal distribution for that pitch, pitcher.
This might not seem like much, but it's a very useful formalism because it specifies the variables we think are relevant and the relationships between them. Here, the relevant dimensions are: pitcher, pitch type, pitch properties. The pitch properties depend on pitch type, and pitch type depends on pitcher.
Of these three variables, gameday gives us the pitch properties (movement, velocity and location), and the pitcher identity. The pitch type variable is a latent (unobserved) variable that we hypothesize mediates the relationship between the pitcher and the pitch parameters. The goal is to use the variables we have observed and the hypothesized relationships to evaluate the latent variable, pitch type.
In the end, the probabilistic model works much like a regression. A regression tries to find the single best linear model (the maximum likelihood estimate for the model parameters). Similarly, the probabilistic model work tries to maximize the likelihood of the observed data, given our model. It simultaneously tries to fit pitch-types to pitchers and pitches to pitch-types.
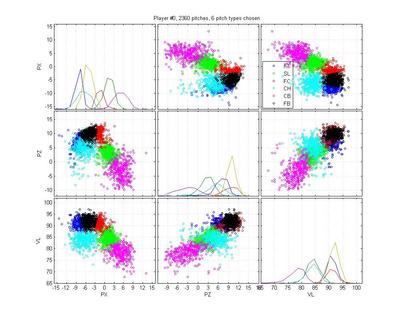
Centers of mass for each pitch type across pitchers, normalized by fastball speed
To illustrate how this works, consider a simple example: two pitchers throw an 85 mph pitch that could be a fastball. For pitcher A, it actually is a fastball and for B it is a change-up. For each pitcher, the model will consider the cluster of pitches that looks most like a fastball (for that pitcher). For the pitcher A, there will be nothing faster than the 85 mph pitch. This will cause the algorithm to shift the FB category down, so that it treats 85 mph pitches as fastballs. It will then push the CH category even further down in search of another cluster. For pitcher B, the 85 mph pitches don't look as fastball-y as his 95 mph pitches, which have to be fastballs. This causes the algorithm to shift the FB category up to 95 mph. The CH category will then sweep in to 85 mph fill the gap. Only by using information about the pitchers other pitches can we successfully discriminate between these two pitch types.
Park Effects
There has been some good work looking at differences in the pitch F/X set-up at different parks. I first corrected all of the pitch F/X data by removing the average park effects for each park-year.
Heuristics
I built in some heuristics to reflect our knowledge of the game. Analysts are very good at pitch classification, so why not just copy them? A brainstorming session over at The Book Blog proposed the idea of classifying the fastest pitch as a FB, and the slowest as a CB, and then classifying other pitches relative to these bounds. That works well with this algorithm because estimating the parameters is an iterative process. So we can first guess which pitches are fastballs, and then use the speed of those fastballs to help us figure out the identity of other pitches. As we iterate, our guesses for which pitches are fastballs will change gradually, as will our estimated fastball speed. If the algorithm works, it will converge on the "true" fastball speed, and allow us to use this information to inform our decision about other pitches.
Results
The goal was to achieve 98% accuracy. We're not there yet, but I'll you decide how far away we are. I've randomly selected some pitchers (I skipped the boring cases where classification was easy) to illustrate it's success. I think this selection represents the strengths and the remaining weaknesses of the model.
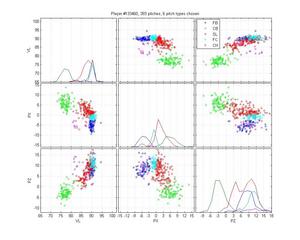
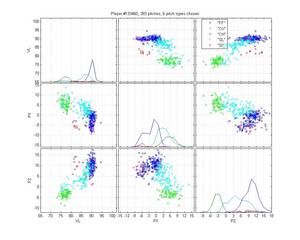
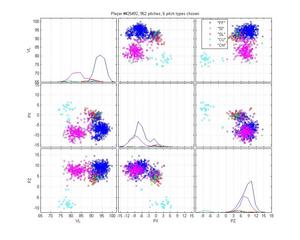
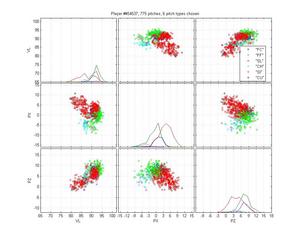
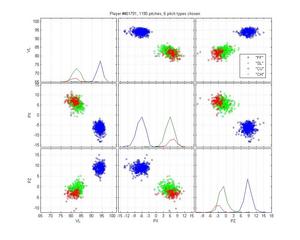
Russ Ortiz
I like Ortiz because he provides a particularly nasty problem for pitch classification (even though the HPM does not perfectly categorize his pitches). His curveball is obvious, as are his change-ups. But he has two very similar fastballs and his slider is right in there too. The MLB classification is pretty poor: they give him one fastball that spreads from 0 to -9 inches of lateral movement; they mix sliders up with both fastballs and curveballs; and some of the change-ups are classified as sinkers. The HPM classifies his fastball into two groups, which looks right to me. It falls prey to one of the problems of the MLB classification, though, by letting the SL cluster nibble on the edge of the FB cluster. That's clearly wrong.
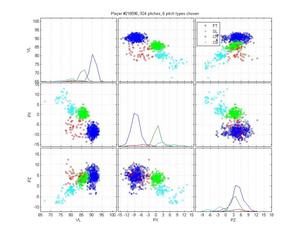
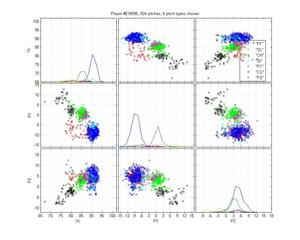
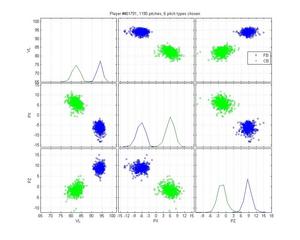
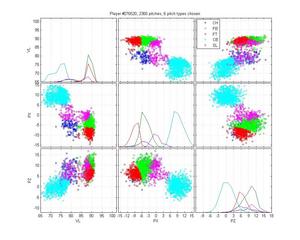
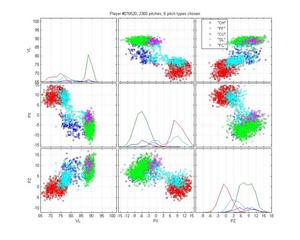
HPM classification (left), MLB classification (right)
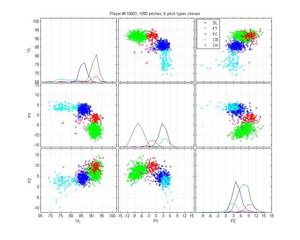
Ryan Madsen
Neither pitch classification system notices that Madsen throws a 2-seamer, but its hard to blame them; it overlaps pretty well with his fastball. The HPM is really solid otherwise, whereas MLB is really confused about his cutter.
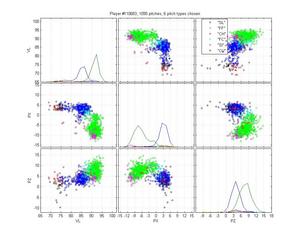
Miguel Batista
Batista poses another interesting problem because he throws a cutter and a sinker and, who knows, there may be a 4-seamer in there too. The MLB classification is pretty poor: it only calls a small portion of his sinkers as sinkers, and none of the cutters as cutters. Instead, it calls some sliders as cutters. It also really confuses curveballs and change-ups. Again, the HPM is not perfect: The curves are nibbling in on the slider cluster, which is clearly wrong. It also may be calling too many pitches change-ups. Hard to say. But the difference is still night-and-day.
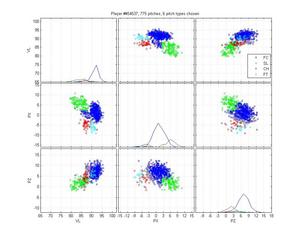
Jared Burton
Burton is an example of a relatively easy case that MLB screws up horribly. Its remarkably inaccurate. The HPM model isn't up to snuff either, but it does better. I honestly can't say how I would classify the cluster below the cutter; is it an extension of his slider cluster? That would be my guess, but with low confidence.
Tim Hudson
The HPM may be overly enthusiastic about the change-ups, and I think the classification of sliders and curveballs is potentially arguable, but overall I'm happy with it. The MLB classification, on the other hand...
Carlos Marmol
Marmol is a really, really easy classification, but MLB still gets it wrong by splitting his slurvy pitch half and half into sliders and curveballs. I don't really care about the labels--we could call it a luxury yacht for all I care--as long as all the pitches of the same type are given the same labels.
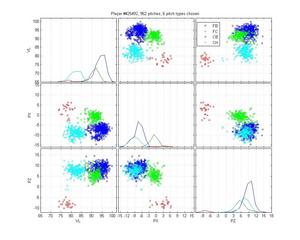
Bronson Arroyo
Arroyo is an absolute nightmare for pitch classification algorithms. I have difficulty figuring out what he actually throws. He has two fastballs, but they have a huge variance and are highly overlapping. What is going on with that change-up? Is it that inconsistent, or is there a ton of noise in these data? His slider and his curve are highly overlapping as well. I don't even want to venture a guess as to the type of the pitches that fall between his fastball and his slider. In this case, the HPM is absolutely clueless and in some ways worse than MLB. It really gets thrown by that train of pitches that straddle the FB-SL divide, which pulls the SL cluster up into the gap between FB, CH and SL. It also doesn't do a good job of separating the FB and FTs. But I always expected some failures, and this is at least an understandable one.
Some Remaining Problems
The biggest problem with this model is that the underlying generative model is wrong. We have to assume that all pitchers throw the same number of pitches. That leads to some problems for some pitchers. The "nibbling" of the corners of a cluster by another pitch-type is caused by extra pitch types that the pitcher doesn't throw sitting between groups.
That leads to a second problem with the model: it tries to maximize the likelihood of the observed data, but it doesn't care if it predicted a lot of pitches in a region where there are none. Essentially we are giving it credit for hits without penalizing for false alarms. This is what causes extra pitch-types to float into the spaces between groups, like in Bronson Arroyo's case.
Third, there is Bronson Arroyo. I think the solution is for him to retire.
Comments
With all the people calculating secondary things such as batting stats vs pitcher's pitch and combination of pitches based on the available classification data, I would expect the team's private statisticians would love to have this to recheck assertions they make, e.g. opponent batter has a pronounced weakness against LHP changeups, when moving a couple of AB's with mistaken classification makes it look normal.
Posted by: Gilbert at October 22, 2009 7:25 AM
Chris - this is great stuff. Thanks for sharing the work.
Two comments
1) Hudson's classifications are more than potentially arguable, those are not all sliders
2) adjusting parks by their average factor is dicey - you have to go down to the game level (or a range of dates) to get it tightened up ... even that is not going to pan out well ... there are plenty examples of game-to-game (even inning-to-inning) changes in system calibration.
Posted by: Harry Pavlidis at October 22, 2009 8:20 AM
Very interesting work, and results! Yeah, looks like a good next step is to try applying techniques for choosing the number of clusters.
Bronson Arroyo uses a wide range of arm slots, doesn't he? That's going to break the Gaussian cluster model -- imagine he has a tight PX and PZ distribution *for a given arm slot*, then as he varies it you get that distribution tracing out a curve in PX-PZ space.
Out of curiosity, how does your system do on sidearm or submarine pitchers, even if they don't vary their arm slot?
Posted by: oki92 at October 22, 2009 10:36 AM
I wonder what would happen if you used a PX'-PZ' coordinate system that's rotated so the pitcher's arm angle is "up". I haven't seen PFX data visualized that way, but it seems like it might normalize out the arm-slot problem.
(The assumption here is that a Chad Bradford curve has "normal" curve spin relative to his hand and arm, he's just turned the whole thing upside down. I don't know if that's true, but it seems plausible.)
Posted by: oki92 at October 22, 2009 10:43 AM